题目内容
18．
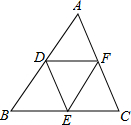如图，在△ABC中，AB=5，BC=6，AC=7，点D，E，F分别是△ABC三边的中点，则△DEF的周长为（ ）| A． | 9 | B． | 10 | C． | 11 | D． | 12 |
分析 根据D、E、F分别是AB、AC、BC的中点，可以判断DF、FE、DE为三角形中位线，利用中位线定理求出DF、FE、DE与AC、AB、CB的长度关系即可解答．
解答 解：∵D、E、F分别是AB、AC、BC的中点，
∴ED、FE、DF为△ABC中位线，
∴DF=$\frac{1}{2}$AC，FE=$\frac{1}{2}$AB，DE=$\frac{1}{2}$BC；
∴DF+FE+DE=$\frac{1}{2}$AC+$\frac{1}{2}$AB+$\frac{1}{2}$BC=$\frac{1}{2}$（AC+BA+CB）=$\frac{1}{2}$×（6+7+5）=9．
故选A．
点评 本题考查了三角形的中位线定理，根据中点判断出中位线，再利用中位线定理是解题的基本思路．
练习册系列答案
相关题目
如图所示，已知CD是△ABC中∠ACB的外角平分线，请说明：∠BAC＞∠B．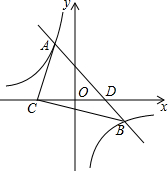
如图，一次函数y=ax+b的图象与反比例函数y=-$\frac{3}{x}$的图象交于A（-1，m）、B（3，n）两点，与x轴交于D点，且C、D两点关于y轴对称．
6．在数轴上与原点的距离小于7的点对应的x值，应满足（ ）
| A． | -7＜x＜7 | B． | x＜-7或x＞7 | C． | x＜7 | D． | x＞7 |
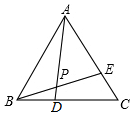如图，△ABC是等边三角形，点D、E分别是BC、AC边上的两点，其中BD=CE，连接AD、BE交于点P
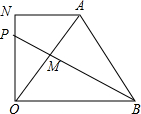如图，在直角梯形ABON中，AN∥BO，∠ANO=90°，点A恰好在线段OB垂直平分线上，P为ON上一点，∠OPB=∠OAB，OA、OB交于点M，若ON=3，求OP+PB的值．
10．某射击运动员练习射击，5次成绩分别是：8、9、7、8、x（单位：环）．下列说法中正确的是（ ）
| A． | 若这5次成绩的中位数为8，则x=8 | B． | 若这5次成绩的众数是8，则x=8 | ||
| C． | 若这5次成绩的方差为8，则x=8 | D． | 若这5次成绩的平均成绩是8，则x=8 |
