��Ŀ����
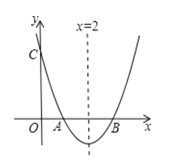
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OCDE����������ֱ���C��3��0����D��3��4����E��0��4��.��AΪ����������߹���C���ҶԳ���![]() ��x���ڵ�B������EC��AC����P��QΪ���㣬���˶�ʱ��Ϊt�롣
��x���ڵ�B������EC��AC����P��QΪ���㣬���˶�ʱ��Ϊt�롣
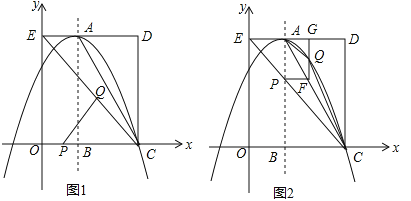
��1��ֱ��д��A�����꣬������������ߵĽ���ʽ��
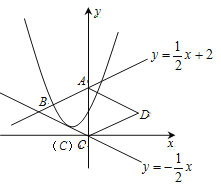
��2����ͼ1�У�����P���߶�OC�ϴӵ�O���C��1����λ/����ٶ��˶���ͬʱ��Q���߶�CE�ϴӵ�C���E��2����λ/����ٶ��˶�����һ���㵽���յ�ʱ����һ������ֹ֮ͣ�˶�����tΪ��ֵʱ��![]() Ϊֱ�������Σ�
Ϊֱ�������Σ�
��3����ͼ2�У�����P�ڶԳ����ϴӵ�B��ʼ���A��2����λ/����ٶ��˶�������P��![]() ����AC�ڵ�F������F��
����AC�ڵ�F������F��![]() �ڵ�G�����������ڵ�Q������AQ��CQ.��tΪ��ֵʱ��
�ڵ�G�����������ڵ�Q������AQ��CQ.��tΪ��ֵʱ��![]() �����������ֵ�Ƕ��٣�
�����������ֵ�Ƕ��٣�
���𰸡���1��A������Ϊ��1��4����![]() ����2����
����2����![]() ��
��![]() ʱ��
ʱ��![]() Ϊֱ�������Σ���3����
Ϊֱ�������Σ���3����![]() ʱ��
ʱ��![]() �����������ֵΪ1.
�����������ֵΪ1.
��������
��1���ɾ��ε����ʿ�ֱ�����A�����꣬���趥��ʽ���̣���C������������������ߵĽ���ʽ��
��2�����������ʾ��P��Q�����꣬�����ô���ϵ�������PQ����ֱ�߽���ʽ��������D���������𰸣�
��3�������ֱ��AC�Ľ���ʽ���ɷֱ���t��ʾ��P���Q������꣬�Ӷ������FQ�ij�������t��ʾ����ACQ��������ٸ��ݶ��κ��������ʿ���������ֵ��
�⣺��1���������ߵĶԳ���![]() ������OCDE����������ֱ���C��3��0����D��3��4����E��0��4��
������OCDE����������ֱ���C��3��0����D��3��4����E��0��4��
���A��������1��4��
�������ߵĽ���ʽΪ��![]()
��C��3��0�����������߽���ʽ���ɵã�![]()
��ã�![]()
�������ߵĽ���ʽΪ��![]() ����
����![]()
��2��������ã�![]() ��
��![]()
��![]()
��![]() ʱ
ʱ
��![]()
��![]() ��ã�
��ã�![]()
��![]() ʱ
ʱ
��![]()
��![]() ��ã�
��ã�![]()
�൱![]() ��
��![]() ʱ��
ʱ��![]() Ϊֱ��������
Ϊֱ��������
��3����A��1��4����C��3��0��
��ֱ��AC�Ľ���ʽΪ��![]()
![]() ��ã�
��ã�![]()
��ֱ��AC�Ľ���ʽΪ��![]()
��P��1��![]() ������
������![]() ����
����![]() �ã�
�ã�![]()
��Q��ĺ�����Ϊ��![]()
��![]() ����
����![]() ����
����![]()
��Q�����������![]()
��![]()
��![]()
![]()
��![]()
![]()
�൱![]() ʱ��
ʱ��![]() �����������ֵΪ1
�����������ֵΪ1

 ����С״Ԫ��������������ϵ�д�
����С״Ԫ��������������ϵ�д�