Question

【题目】如图，在平面直角坐标系中，直线与轴交于点，与轴交于点，点在轴正半轴上，．

（1）求直线的解析式；

（2）点是射线上一点，连接，设点的横坐标为，的面积为，求与的函数解析式，并直接写出自变量的取值范围；

（3）在（2）的条件下，与轴交于点，连接，过点作的垂线，垂足为点，直线交轴于点，交线段于点，直线交轴于点，当时，求直线的解析式．

Answer 1

【答案】（1）；（2），；（3）

【解析】

（1）求出点A、B的坐标，从而得出△ABO是等腰直角三角形，再根据可得△OCB也是等腰直角三角形，从而可求得点C的坐标，将点B、C代入可求得解析式；

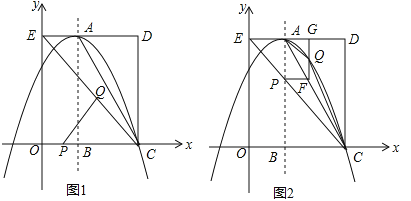
（2）存在2种情况，一种是点D在线段BC上，另一种是点D在线段BC的延长线上，分别利用三角形的面积公式可求得；

（3）如下图，先证，从而推导出，进而得到，同理还可得，，然后利用可得到N、D的坐标，代入即可求得．

解：（1）直线与轴交于点，与轴交于点，

，．．

，，

，

，．设直线的解析式为，

将、两点坐标代得

解得

直线的解析式为．

（2）点是射线上一点，点的横坐标为，

，．

如下图，过点作于点，当点在线段上时，

，

；

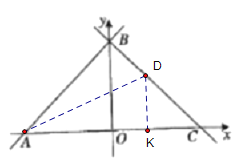
如下图，当点在线段的延长线上时，

，．

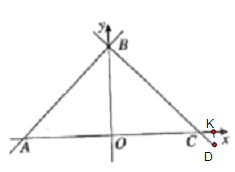
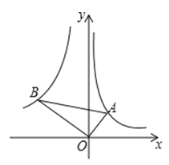
（3）如图，延长交于点，连接交于点，交轴于点．

，．

，，．

．．

．．．，

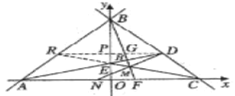
．，∠MRB

．．，

．．

同理．．

∵．．

，

，，，．

．，．．

，．

设直线的解析式为，将、两点代入，

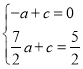
解得

直线的解析式为．