题目内容
19. 如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=2$\sqrt{2}$,CD=$\sqrt{2}$,点P在四边形ABCD的边上.若点P到BD的距离为$\frac{3}{2}$,则点P的个数为( )
如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=2$\sqrt{2}$,CD=$\sqrt{2}$,点P在四边形ABCD的边上.若点P到BD的距离为$\frac{3}{2}$,则点P的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 首先作出AB、AD边上的点P(点A)到BD的垂线段AE,即点P到BD的最长距离,作出BC、CD的点P(点C)到BD的垂线段CF,即点P到BD的最长距离,由已知计算出AE、CF的长与$\frac{3}{2}$比较得出答案.
解答  解:过点A作AE⊥BD于E,过点C作CF⊥BD于F,
解:过点A作AE⊥BD于E,过点C作CF⊥BD于F,
∵∠BAD=∠ADC=90°,AB=AD=2$\sqrt{2}$,CD=$\sqrt{2}$,
∴∠ABD=∠ADB=45°,
∴∠CDF=90°-∠ADB=45°,
∵sin∠ABD=$\frac{AE}{AB}$,
∴AE=AB•sin∠ABD=2$\sqrt{2}$•sin45°
=2$\sqrt{2}$•$\frac{\sqrt{2}}{2}$=2>$\frac{3}{2}$,
CF=1<$\frac{3}{2}$
所以在AB和AD边上有符合P到BD的距离为$\frac{3}{2}$的点2个,
故选A.
点评 本题考查了解直角三角形和点到直线的距离,解题的关键是先求出各边上点到BD的最大距离比较得出答案.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
4.a2的算术平方根一定是( )
| A. | a | B. | |a| | C. | $\sqrt{a}$ | D. | -a |
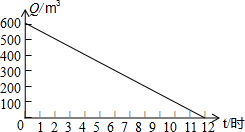 河道的剩水量Q(米3)和水泵抽水时间t(时)的关系图象如图,则水泵抽水前,河道内有600米3的水,水泵最多抽12小时,水泵抽8小时后,河道剩水量是200米3.
河道的剩水量Q(米3)和水泵抽水时间t(时)的关系图象如图,则水泵抽水前,河道内有600米3的水,水泵最多抽12小时,水泵抽8小时后,河道剩水量是200米3.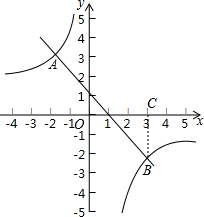 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于点A(-2,3),B(3,n)两点.
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于点A(-2,3),B(3,n)两点. 如图,在平面直角坐标系中,抛物线y=a(x-1)2+4与x轴交于点A、B两点,与y轴交于点C,且点B的坐标为(3,0),点P在这条抛物线上,且不与B、C两点重合.过点P作y轴的垂线与射线BC交于点Q,以PQ为边作Rt△PQF,使∠PQF=90°,点F在点Q的下方,且QF=1.设线段PQ的长度为d,点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=a(x-1)2+4与x轴交于点A、B两点,与y轴交于点C,且点B的坐标为(3,0),点P在这条抛物线上,且不与B、C两点重合.过点P作y轴的垂线与射线BC交于点Q,以PQ为边作Rt△PQF,使∠PQF=90°,点F在点Q的下方,且QF=1.设线段PQ的长度为d,点P的横坐标为m. 如图,小聪与小慧玩跷跷板,跷跷板支架高EF为0.6米,E是AB的中点,那么小聪能将小慧翘起的最大高度BC等于1.2米.
如图,小聪与小慧玩跷跷板,跷跷板支架高EF为0.6米,E是AB的中点,那么小聪能将小慧翘起的最大高度BC等于1.2米.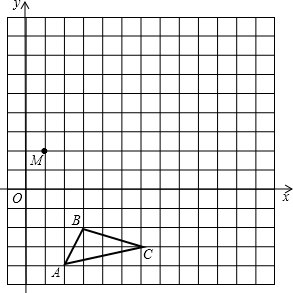 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).
在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).