题目内容
如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE.
(1)求证: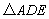 ≌
≌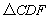 .
.
(2)把 向左平移,使
向左平移,使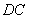 与
与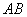 重合,得
重合,得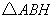 ,
,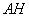 交
交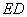 于点
于点 .请判断AH与ED的位置关系,并说明理由.
.请判断AH与ED的位置关系,并说明理由.
(3)求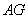 的长.
的长.
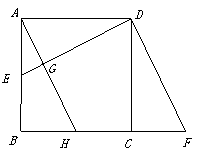 |
解:(1)由已知正方形ABCD得AD=DC
 ,
,
又∵AE=CF
∴ .
.
(2)AH⊥ED
理由:由(1)和平移性质可知 ,∵
,∵ ,
,
∴ ∴
∴ .即AH⊥ED
.即AH⊥ED
(3)由已知AE=1,AD=2,
∴ ,
,
∴
即 ,∴
,∴ .
.
(注:用三角形相似解的,计算ED,判定相似,求解AG各得1分)

练习册系列答案
相关题目
 线y=2x+4与
线y=2x+4与 轴、
轴、 轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD,点D在双曲线
轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD,点D在双曲线 上,将正方形ABCD沿
上,将正方形ABCD沿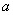 个单位长度后,点C恰好落在此双曲线上,则
个单位长度后,点C恰好落在此双曲线上,则

 如图(a),点A、B在直线l的同侧,要在直线l上找一点C,使AC与BC的距离之和最小,我们可以作出点B关于l的对称点B′,连接A B′与直线l交于点C,则点C即为所求.
如图(a),点A、B在直线l的同侧,要在直线l上找一点C,使AC与BC的距离之和最小,我们可以作出点B关于l的对称点B′,连接A B′与直线l交于点C,则点C即为所求. ),已知,⊙O的直径CD为4,点A 在⊙O 上,∠ACD=30°,B 为弧AD 的中点,P为直径CD上一动点,则BP+AP的最小值为__________.
),已知,⊙O的直径CD为4,点A 在⊙O 上,∠ACD=30°,B 为弧AD 的中点,P为直径CD上一动点,则BP+AP的最小值为__________.  -20120=
-20120= 


 其中x=-6.
其中x=-6.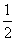 x2+x+c与x轴没有交点.
x2+x+c与x轴没有交点.