Question

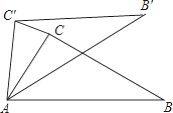
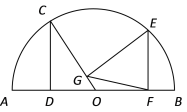
【题目】如图，O是半圆的圆心，半径为4．C、E是圆上的两点，CD⊥AB，EF⊥AB，EG⊥CO．若∠COA=60°，则FG=______．

Answer 1

【答案】

【解析】

首先根据四点共圆的性质得出GOFE四点共圆，进而求出△GHF∽△OGE，再利用GH∥CD，得出==，即可求出答案．

解：作GH⊥AB，连接EO．

∵EF⊥AB，EG⊥CO，

∴∠EFO=∠EGO=90°，

∴G、O、F、E四点共圆，

所以∠GFH=∠OEG，

又∵∠GHF=∠EGO，

∴△GHF∽△OGE，

∵CD⊥AB，GH⊥AB，

∵GH∥CD，

∴==，

又∵CO=EO，

∴CD=FG．

在Rt△CDO中，OC=4，∠COD=60，

∴CD=sin60·OC=×4=2，

∴FG=2..

故答案为：2.