题目内容
 已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AD的延长线相交于点F,且AD=2
已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AD的延长线相交于点F,且AD=2| 7 |
| 3 |
| 4 |
(1)求证:CD∥BF;
(2)求弦CD的长;
(3)求⊙O的半径.
分析:(1)由BF是⊙O的切线得到AB⊥BF,而AB⊥CD,由此即可证明CD∥BF;
(2)根据圆周角定理可得∠A=∠BCD,由于sin∠BCD=
,所以sin∠A=
,而AD=2
,由此求出DE也就求出了CD;
(3)连接BD,由AB是直径得到∠ADB=90°,而∠BCD=∠BAD,所以sin∠BAD=
=
,再利用勾股定理即可求出AB,进而求出圆的半径.
(2)根据圆周角定理可得∠A=∠BCD,由于sin∠BCD=
| 3 |
| 4 |
| 3 |
| 4 |
| 7 |
(3)连接BD,由AB是直径得到∠ADB=90°,而∠BCD=∠BAD,所以sin∠BAD=
| BD |
| AB |
| 3 |
| 4 |
解答:(1)证明:
∵BF是⊙O的切线,
∴AB⊥BF,
∵AB⊥CD,
∴CD∥BF;
解:(2)∵∠BCD=∠BAD,
∴sin∠DAE=sin∠BCD=
,AD=2
,
∴
=
,
∵AD=2
,
∴DE=
,
∵AE⊥DE,
∴CE=DE,
∴CD=2ED=3
;
(3)连结BD,
∵AB是直径,
∴∠ADB=90°,
∴sin∠BAD=
=
,
∴AB=
BD,
∵AD=2
,
由勾股定理得BD=6,AB=8,
∴⊙O的半径为4.
∵BF是⊙O的切线,
∴AB⊥BF,

∵AB⊥CD,
∴CD∥BF;
解:(2)∵∠BCD=∠BAD,
∴sin∠DAE=sin∠BCD=
| 3 |
| 4 |
| 7 |
∴
| DE |
| AD |
| 3 |
| 4 |
∵AD=2
| 7 |
∴DE=
3
| ||
| 2 |
∵AE⊥DE,
∴CE=DE,
∴CD=2ED=3
| 7 |
(3)连结BD,
∵AB是直径,
∴∠ADB=90°,
∴sin∠BAD=
| BD |
| AB |
| 3 |
| 4 |
∴AB=
| 4 |
| 3 |
∵AD=2
| 7 |
由勾股定理得BD=6,AB=8,
∴⊙O的半径为4.
点评:本题考查了圆的切线性质,勾股定理的运用及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 7、已知⊙O的直径AB与弦AC的夹角为35°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )
7、已知⊙O的直径AB与弦AC的夹角为35°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )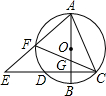 如图,已知⊙O的直径AB与弦CD相交于点G,E是CD延长线上的一点,连接AE交⊙O于F,连接AC、CF,若AC2=AF•AE.
如图,已知⊙O的直径AB与弦CD相交于点G,E是CD延长线上的一点,连接AE交⊙O于F,连接AC、CF,若AC2=AF•AE. 如图,已知⊙O的直径AB与弦AC的夹角∠CAB=27°,过点C作⊙O的切线交AB延长线于点D,则∠ADC的度数为( )
如图,已知⊙O的直径AB与弦AC的夹角∠CAB=27°,过点C作⊙O的切线交AB延长线于点D,则∠ADC的度数为( ) (2010•邢台二模)如图,已知⊙O的直径AB与弦AC的夹角为31°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )
(2010•邢台二模)如图,已知⊙O的直径AB与弦AC的夹角为31°,过C点的切线PC与AB的延长线交于点P,则∠P等于( ) 如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AC的延长线相交于点F,且AC=8,tan∠BDC=
如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AC的延长线相交于点F,且AC=8,tan∠BDC=