��Ŀ����
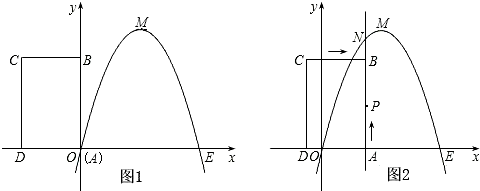
��ͼ1����֪����ABCD�Ķ���A���O�غϣ�AD��AB�ֱ���x�ᡢy���ϣ���AD=2��AB=3�������� ��������ԭ��O��x������һ��E��4,0��
��������ԭ��O��x������һ��E��4,0��
ͼ1 ͼ2
��1����xȡ��ֵʱ���������ߵ����ֵ�Ƕ��٣�
��2��������ABCD��ÿ��1����λ���ȵ��ٶȴ�ͼ1��ʾ��λ����x�������������ƽ���ƶ���ͬʱһ����PҲ����ͬ���ٶ��ӵ�A������B�����ƶ�.�������˶���ʱ��Ϊt�루0��t��3����ֱ��AB��������ߵĽ���ΪN����ͼ2��ʾ��.
�� �� ʱ���жϵ�P�Ƿ���ֱ��ME�ϣ���˵�����ɣ�
ʱ���жϵ�P�Ƿ���ֱ��ME�ϣ���˵�����ɣ�
�� ��P��N��C��DΪ����Ķ��������Ƿ����Ϊ5�����п��ܣ������ʱN������ꣻ�����ܣ���˵�����ɣ�
��1���������� ��������ԭ��O��0,0���͵�E��4,0��
��������ԭ��O��0,0���͵�E��4,0��
�ʿɵ�c=0,b=4���������ߵĽ���ʽΪ
��

�õ�x=2ʱ���������ߵ����ֵ��4.
��2���� ��P����ֱ��ME��.��֪M�������Ϊ(2,4)��E�������Ϊ(4,0)��
��ֱ��ME�Ĺ�ϵʽΪy=kx+b.
���ǵ� �����
�����
����ֱ��ME�Ĺ�ϵʽΪy="-2x+8."
����֪�����ã��� ʱ��OA=AP=
ʱ��OA=AP= ��
��
�� P������겻����ֱ��ME�Ĺ�ϵʽy=-2x+8.
�� �� ʱ����P����ֱ��ME��.
ʱ����P����ֱ��ME��.
����P��N��C��DΪ����Ķ�����������Ϊ5
�� ��A��x��ķǸ������ϣ���N���������ϣ� �� OA=AP=t.
�� ��P��N������ֱ�Ϊ(t,t)��(t,-t 2+4t)
�� AN=-t 2+4t (0��t��3) ,�� AN-AP=(-t 2+4 t)- t=-t 2+3 t=t(3-t)��0 ,
�� PN=-t 2+3 t
��������PN=0����t=0��t=3ʱ���Ե�P��N��C��DΪ����Ķ�����������Σ��������εĸ�ΪAD���� S= DC��AD=
DC��AD= ��3��2=3.
��3��2=3.
��������PN��0ʱ���Ե�P��N��C��DΪ����Ķ����������.
�� PN��CD��AD��CD��
�� S= (CD+PN)��AD=
(CD+PN)��AD= [3+(-t 2+3 t)]��2=-t 2+3 t+3
[3+(-t 2+3 t)]��2=-t 2+3 t+3
��-t 2+3 t+3=5ʱ�����t=1��2
��1��2����0��t��3��Χ�ڣ�����P��N��C��DΪ����Ķ�������Ϊ5
������������t=1��2ʱ���Ե�P��N��C��DΪ����Ķ�������Ϊ5��
��t=1ʱ����ʱN������꣨1,3��
��t=2ʱ����ʱN������꣨2,4��
����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�