Question

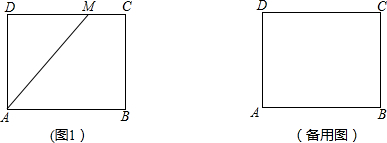
（2013•下关区一模）如图1，已知矩形ABCD中，AB=5，AD=4，点M在线段CD上，连接AM．把矩形沿一条直线EF折叠，使点A与点M重合．

（1）作出直线EF （保留作图痕迹，不写作法）；
（2）当直线EF经过点B时，连接BM，求△BCM的面积．

Answer 1

分析：（1）根据翻折的性质，对应点的连线被对称轴垂直平分，所以，作出AM的垂直平分线即为直线EF；
（2）根据线段垂直平分线上的点到线段两端点的距离相等可得BM=AB，再根据勾股定理列式求出CM，然后根据三角形的面积公式列式计算即可得解．

解答：解：（1）直线EF如图所示：

（2）∵AM关于直线EF对称，
∴EF是AM的垂直平分线，
∴BM=AB=5，
∵矩形的对边BC=AD=4，
∴CM=

BM2-BC2

=

52-42

=3，
∴△BCM的面积=

1

2

CM•BC=

1

2

×3×4=6．

点评：本题考查了正方形的性质，翻折变换的性质，主要利用了对称点的连线被对称轴垂直平分，线段垂直平分线上的点到线段两端点的距离相等的性质．