Question

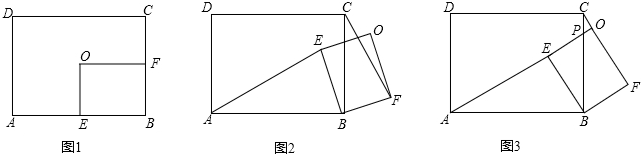
（2012•宝安区二模）如图1，已知矩形ABCD中，AB=

4

3

BC，O是矩形ABCD的中心，过点O作OE⊥AB于E，作OF⊥BC于F，得矩形BEOF．
（1）线段AE与CF的数量关系是

AE=

4

3

CF；

，直线AE与CF的位置关系是

AE⊥CF

；
（2）固定矩形ABCD，将矩形BEOF绕点B顺时针旋转到如图2的位置，连接AE、CF．那么（1）中的结论是否依然成立？请说明理由；
（3）若AB=8，当矩形BEOF旋转至点O在CF上时（如图3），设OE与BC交于点P，求PC的长．

Answer 1

分析：（1）根据O是矩形ABCD的中心，OE⊥AB于E，OF⊥BC于F可知，四边形OEBF为矩形，可推知各线段的数量及位置关系；
（2）延长AE交BC于H，交CF于G，由已知得BE=

1

2

AB，BF=

1

2

BC进而得到

BE

AB

=

BF

BC

=

1

2

，构造相似三角形△ABE和△CBF，根据相似三角形的性质进行判断；
（3）根据已知条件，利用勾股定理求出CF的长，进而求出OC的长，判断出△BPE∽△CPO，根据相似三角形的性质即可求出PC的长．

解答：解：（1）∵O是矩形ABCD的中心，OE⊥AB于E，OF⊥BC于F，
∴AE=

1

2

AB，CF=

1

2

BC，
∵AB=

4

3

BC，
∴

1

2

AB=

1

2

×

4

3

BC，即AE=

4

3

CF；
∵AB⊥BC，点E、F分别是AB、BC上的点，
∴AE⊥CF；
故答案为AE=

4

3

CF；AE⊥CF；

（2）（1）中的结论仍然成立．
如图1，延长AE交BC于H，交CF于G，
由已知得BE=

1

2

AB，BF=

1

2

BC
∴

BE

AB

=

BF

BC

=

1

2

∵∠ABC=∠EBF=90°，
∴∠ABE=∠CBF，
∴△ABE∽△CBF，
∴∠BAE=∠BCF，

AE

CF

=

AB

BC

=

4

3

，
∵∠BAE+∠AHB=90°，∠AHB=∠CHG，
∴∠BCF+∠CHG=90°
∴∠CGH=180°-（∠BCF+∠CHG）=90°，
∴AE⊥CF，且AE=

4

3

CF．

（3）∵AB=

4

3

BC，AB=8，
∴BC=6，
∴BE=OF=4，BF=OE=3，
∵点O在CF上，
∴∠CFB=90°，
∴CF=

BC2-BF2

=

62-32

=3

3

，
∴OC=CF-OF=3

3

-4，
∵∠CPO=∠BPE，∠PEB=∠POC=90°，
∴△BPE∽△CPO，
∴

CP

BP

=

OC

BE

，
设CP=x，则BP=6-x，
∴

x

6-x

=

3 3 -4

4

，
解得：x=

18-8 3

3

，
∴PC=

18-8 3

3

．

点评：本题考查了相似形综合问题，借助矩形的性质，做出适当辅助线可有助于问题的解答，由于综合性较强，故难度较大．