题目内容
14.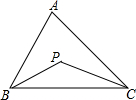 如图,在三角形ABC中,∠ABC与∠ACB的平分线交于点P,设∠A=x°,∠BPC=y°,当∠A变化时,求y与x之间的函数关系式.并判断y是不是x的一次函数.
如图,在三角形ABC中,∠ABC与∠ACB的平分线交于点P,设∠A=x°,∠BPC=y°,当∠A变化时,求y与x之间的函数关系式.并判断y是不是x的一次函数.
分析 先根据角平分线定义得到∠PBC=$\frac{1}{2}$∠ABC,∠PCB=$\frac{1}{2}$∠ACB,则利用三角形内角和得∠BPC=180°-$\frac{1}{2}$(∠ABC+∠ACB),而∠ABC+∠ACB=180°-∠A,所以∠BPC=90°+$\frac{1}{2}$∠A,即y=90°+$\frac{1}{2}$x,然后根据一次函数的定义可判断y是x的一次函数.
解答 解:∵∠ABC与∠ACB的平分线交于点P,
∴∠PBC=$\frac{1}{2}$∠ABC,∠PCB=$\frac{1}{2}$∠ACB,
∴∠BPC=180°-∠PBC-∠PCB=180°-$\frac{1}{2}$(∠ABC+∠ACB),
而∠ABC+∠ACB=180°-∠A,
∴∠BPC=180°-$\frac{1}{2}$(180°-∠A)=90°+$\frac{1}{2}$∠A,
即y=90°+$\frac{1}{2}$x,
∴y是x的一次函数.
点评 本题考查了三角形内角和定理:三角形内角和是180°.三角形内角和主要用在求三角形中角的度数.也考查了一次函数的定义.

练习册系列答案
相关题目

 已知:如图,在平面直角坐标系中,正方形ABCD的边长为8.求出AC和BD的长度,并直接写出它的四个顶点A、B、C、D的坐标.
已知:如图,在平面直角坐标系中,正方形ABCD的边长为8.求出AC和BD的长度,并直接写出它的四个顶点A、B、C、D的坐标.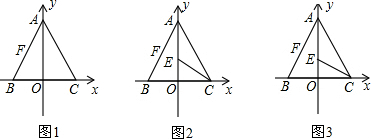
 如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,求证:∠APB=2∠BAC.
如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,求证:∠APB=2∠BAC.