题目内容
8.我们知道简便计算的好处,事实上,简便计算在好多地方都存在,观察下列等式:152=1×2×100+25=225
252=2×3×100+25=625
352=3×4×100+25=1225
(1)根据上述各式反应出的规律填空:952=9×10×100+25=9025
(2)设这类等式左边两位数的十位数字为n,请用一个含n的代数式表示其结果(n5)2=n×(n+1)×100+25=100n(n+1)+25.
分析 (1)根据152=1×2×100+25=225,252=2×3×100+25=625,352=3×4×100+25=1225,…,可得952=9×10×100+25,据此解答即可.
(2)根据152=1×2×100+25=225,252=2×3×100+25=625,352=3×4×100+25=1225,…,可得(a5)2=a×(a+1)×100+25,据此解答即可.
解答 解:(1)∵152=1×2×100+25=225,252=2×3×100+25=625,352=3×4×100+25=1225,…,
∴952=9×10×100+25=9025.
(2)∵152=1×2×100+25=225,252=2×3×100+25=625,352=3×4×100+25=1225,…,
∴(n5)2=n×(n+1)×100+25=100n(n+1)+25.
故答案为:9×10×100+25=9025;(n5)2=n×(n+1)×100+25=100n(n+1)+25.
点评 此题考查数字的变化规律,找出数字之间的联系,得出运算规律解决问题.

练习册系列答案
相关题目
 如图,⊙O中,BD为⊙O直径,弦AD长为3,AB长为5,AC平分∠DAB,则弦AC的长为4$\sqrt{2}$.
如图,⊙O中,BD为⊙O直径,弦AD长为3,AB长为5,AC平分∠DAB,则弦AC的长为4$\sqrt{2}$.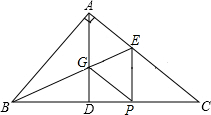 如图,在Rt△ABC中,AD是高线,BE平分∠ABC交AC于E,交AD于G,过E作EP⊥BC于P,连接GP,请问四边形AGPE是什么四边形?为什么?
如图,在Rt△ABC中,AD是高线,BE平分∠ABC交AC于E,交AD于G,过E作EP⊥BC于P,连接GP,请问四边形AGPE是什么四边形?为什么?
 如图,∠GEF和∠DFE的角平分线相交于点H,AB∥CD,∠B=∠D,求证:EH⊥HF.
如图,∠GEF和∠DFE的角平分线相交于点H,AB∥CD,∠B=∠D,求证:EH⊥HF.