题目内容
如图是已建设封顶的16层楼房和它的塔吊示意图，吊臂AG与地面EH平行，测得点A到楼顶D点的距离为5米，每层楼高3.5米，在吊臂上有一点B，AB=16米，在C点测得A点的俯角（∠MCA）为20°，B点的俯角（∠MCB）为40°，AE、CH都垂直于地面，求塔吊的高CH的长（结果精确到0.1米）．（参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36，sin40°≈0.64，cos40°≈0.77，tan40°≈0.84）考点：解直角三角形的应用-仰角俯角问题
专题：
分析：由题意，判断出AB=BC，求出CG的长，根据楼高求出GH的长，CG+HG即为CH的长．
解答：解：根据题意得，DE=3.5×16=56米，AB=EF=16米，
∵∠ACB=∠CBG-∠CAB=20°，
∴∠ACB=∠CAB，
∴CB=AB=16米，
在Rt△GBC中，CG=BC•sin40°=16×0.64=10.24米，
∴CH=CG+HG=CG+DE+AD=10.24+56+5=71.24≈71.2米，
∴塔吊的高CH的长是71.2米．
∵∠ACB=∠CBG-∠CAB=20°，
∴∠ACB=∠CAB，
∴CB=AB=16米，
在Rt△GBC中，CG=BC•sin40°=16×0.64=10.24米，
∴CH=CG+HG=CG+DE+AD=10.24+56+5=71.24≈71.2米，
∴塔吊的高CH的长是71.2米．
点评：本题考查了仰角和俯角问题，将CG的长转化为解直角三角形的问题是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，反比例函数
如图所示，在平面直角坐标中，抛物线的顶点P到x轴的距离是4，抛物线与x轴相交于O、M两点，OM=4；矩形ABCD的边BC在线段的OM上，点A、D在抛物线上．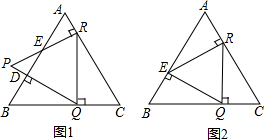
如图1，D是边长为8cm的等边△ABC的边AB上的一点，DQ⊥AB交边BC于点Q，RQ⊥BC交边AC于点R，RP⊥AC交边AB于点E，交QD的延长线于点P．
