题目内容
3.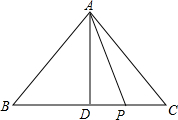 如图,在△ABC中,AB=AC=5,BC=6,AD⊥BC.
如图,在△ABC中,AB=AC=5,BC=6,AD⊥BC.(1)求AD的长;
(2)若点P是BC边上的任意一点(不与B、C两点重合),试求AP2+PB•PC的值;
(3)若点P是BC的延长线上的任意一点,请直接写出AP2-PB•PC的值.
分析 (1)由等腰三角形的性质和勾股定理即可得出结果;
(2)利用勾股定理,借助于平方差公式即可证明;
(3)同(2).
解答 解:(1)∵AB=AC=5,BC=6,AD⊥BC,
∴BD=CD=3,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4;
(2)∵AB=AC,
∴BD=CD
在Rt△ABD中,AB2=AD2+BD2①
在Rt△APD中,AP2=AD2+PD2②
①-②得:AB2-AP2=BD2-PD2=(BD+PD)(BD-PD)=PC•BP,
∴AP2+PB•PC=AB2=25;
(3)若点P是BC的延长线上的任意一点,同(2)得:AP2-PB•PC=AB2=25.
点评 本题主要考查勾股定理、等腰三角形性质;熟练掌握等腰三角形的性质和勾股定理是解决问题的关键.

练习册系列答案
相关题目
 如图,已知五边形ABCDE中,AB∥CD,求x的度数.
如图,已知五边形ABCDE中,AB∥CD,求x的度数.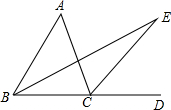 如图所示,∠ACD是△ABC的外角,∠A=40°,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.
如图所示,∠ACD是△ABC的外角,∠A=40°,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.