题目内容
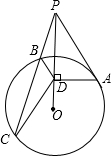如图，P是⊙O外一点，PA切⊙O于A，PBC是⊙O的割线，AD⊥PO于D、求证：| PB |
| BD |
| PC |
| CD |
分析：所证比例线段不是对应边，故不能通过判定△POB与△PCD相似证明．PA2=PD•PO=PB•PC，再易证△PCD∽△POB，根据对应边的比相等，即可证得．
解答：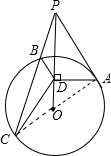
解：连接OA，OC，
∵PA是切线，
∴∠PAO=∠PDA=90°，
又∵∠APD=∠OPA，
∴△APD∽OPA，
∴
=
，
∴PA2=PD•PO，
又∵PA是切线，
∴PA2=PB•PC
∴PA2=PD•PO=PB•PC
又∵∠CPD=∠OPB，
∴△PCD∽△POB
∴
=
=
又△POC∽△PBD，则
=
∴
=
．
解：连接OA，OC，∵PA是切线，
∴∠PAO=∠PDA=90°，
又∵∠APD=∠OPA，
∴△APD∽OPA，
∴
| PD |
| PA |
| PA |
| PO |
∴PA2=PD•PO，
又∵PA是切线，
∴PA2=PB•PC
∴PA2=PD•PO=PB•PC
又∵∠CPD=∠OPB，
∴△PCD∽△POB
∴
| PC |
| CD |
| PO |
| OB |
| PO |
| OC |
又△POC∽△PBD，则
| PO |
| OC |
| PB |
| BD |
∴
| PB |
| BD |
| PC |
| CD |
点评：四点共圆既是一类问题，又是平面几何中一个重要的证明方法，它和证明三角形全等和相似三角形有着同等重要的地位，这是因为，某四点共圆，不但与这四点相联系的条件集中或转移，而且可直接运．用圆的性质为解题服务．
练习册系列答案
相关题目
如图，P是⊙O外一点，PA切⊙O于A，AB是⊙O的直径，PB交⊙O于C，若PA=2cm，∠B=30°，求出图中阴影部分的面积．
（2013•重庆） 如图，P是⊙O外一点，PA是⊙O的切线，PO=26cm，PA=24cm，则⊙O的周长为（ ）
（2012•顺义区二模）已知：如图，P是⊙O外一点，PA切⊙O于点A，AB是⊙O的直径，BC∥OP交⊙O于点C．
如图，P是⊙O外一点，PA、PB切⊙O于点A、B，点C在优弧AB上，若么P=68°，则∠ACB等于（ ）
如图，P是⊙O外一点，PA和PB是⊙O的切线，A，B为切点，P O与AB交于点M，过M任作⊙O的弦CD．