题目内容
设a、b、c、d都不等于0,并且
=
≠1,按照下面的步骤探究
和
关系.
(1)请你任意取3组a、b、c、d的值,通过计算猜想
和
之间的关系;
(2)证明你的猜想.
| a |
| b |
| c |
| d |
| a+b |
| a-b |
| c+d |
| c-d |
(1)请你任意取3组a、b、c、d的值,通过计算猜想
| a+b |
| a-b |
| c+d |
| c-d |
(2)证明你的猜想.
分析:(1)可取a=1,b=2,c=2,d=4;a=1,b=2,c=3,d=6;a=2,b=3,c=6,d=9,再分别代入
和
中进行计算,由计算结果可得到
和
的关系是相等;
(2)由于a、b、c、d都不等于0,并且
=
≠1,则a=
•b,然后代入
,利用分式的基本性质化简即可得到
.
| a+b |
| a-b |
| c+d |
| c-d |
| a+b |
| a-b |
| c+d |
| c-d |
(2)由于a、b、c、d都不等于0,并且
| a |
| b |
| c |
| d |
| c |
| d |
| a+b |
| a-b |
| c+d |
| c-d |
解答:解:(1)当a=1,b=2,c=2,d=4时,
=
=-3,
=
=-3;当a=1,b=2,c=3,d=6时,
=
=-3,
=
=-3;当a=2,b=3,c=6,d=9时,
=
=-5,
=
=-5;
结论为
=
;
(2)证明:∵a、b、c、d都不等于0,并且
=
≠1,
∴a=
•b,
∴
=
=
=
.
| a+b |
| a-b |
| 1+2 |
| 1-2 |
| c+d |
| c-d |
| 2+4 |
| 2-4 |
| a+b |
| a-b |
| 1+2 |
| 1-2 |
| c+d |
| c-d |
| 3+6 |
| 3-6 |
| a+b |
| a-b |
| 2+3 |
| 2-3 |
| c+d |
| c-d |
| 6+9 |
| 6-9 |
结论为
| a+b |
| a-b |
| c+d |
| c-d |
(2)证明:∵a、b、c、d都不等于0,并且
| a |
| b |
| c |
| d |
∴a=
| c |
| d |
∴
| a+b |
| a-b |
| ||
|
| ||
|
| c+d |
| c-d |
点评:本题考查了分式的性质:分式的分子和分母同乘以(或除以)一个不为零的数,分式的值不变.也考查了等式的性质.

练习册系列答案
相关题目
设有理数a、b、c都不为零,且a+b+c=0,则
+
+
的值是( )
| 1 |
| b2+c2-a2 |
| 1 |
| c2+a2-b2 |
| 1 |
| a2+b2-c2 |
| A、正数 | B、负数 | C、零 | D、不能确定 |
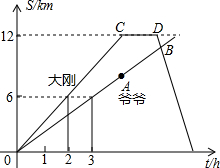 km的B处与爷爷相遇,求大刚下山时的速度.
km的B处与爷爷相遇,求大刚下山时的速度. ,按照下面的步骤探究
,按照下面的步骤探究 和
和 关系.
关系.