Question

【题目】如图，直线y=kx与双曲线y=﹣交于A（x1，y1），B（x2，y2）两点，则2x1y2﹣8x2y1的值为（ ）

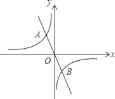
A. ﹣6 B. ﹣12 C. 6 D. 12

Answer 1

【答案】B

【解析】

（解法一）将一次函数解析式代入反比例函数解析式中得出关于x的一元二次方程，解方程即可得出A、B点的横坐标，再结合一次函数的解析式即可求出点A、B的坐标，将其代入2x1y2-8x2y1中即可得出结论．
（解法二）根据正、反比例函数的对称性，找出x1=-x2、y1=-y2，将其代入2x1y2-8x2y1中利用反比例函数图象上点的坐标特征，即可求出结论．

（解法一）将y=kx代入到y=- 中得：
kx=-，即kx2=-2，
解得：x1=- ，x2=，
∴y1=kx1=，y2=kx2=-，
∴2x1y2-8x2y1=2×（-）×（-）-8××=-12．
（解法二）由正、反比例函数的对称性，可知：x1=-x2，y1=-y2，
∴2x1y2-8x2y1=-2x1y1+8x1y1=6x1y1．
∵x1y1=-2，
∴2x1y2-8x2y1=6x1y1=-12．
故选：B．