题目内容
 如图,在反比例函数
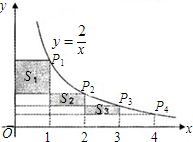
如图,在反比例函数 (x>0)的图象上,有点P1,P2,P3,P4,…Pn,Pn+1,它们的横坐标依次为1,2,3,4…n,n+1,分别过这些点作x轴与y轴的垂线,构成若干个矩形,所构成的阴影部分的面积从左到右依次为S1,S2,S3…Sn,则S1+S2+S3+…+Sn=________.
(x>0)的图象上,有点P1,P2,P3,P4,…Pn,Pn+1,它们的横坐标依次为1,2,3,4…n,n+1,分别过这些点作x轴与y轴的垂线,构成若干个矩形,所构成的阴影部分的面积从左到右依次为S1,S2,S3…Sn,则S1+S2+S3+…+Sn=________.

分析:求出P1、P2、P3、P4…的纵坐标,从而可计算出S1、S2、S3、S4…的高,进而求出S1、S2、S3、S4…,从而得出S1+S2+S3+…+Sn的值.
解答:当x=1时,P1的纵坐标为2,
当x=2时,P2的纵坐标1,
当x=3时,P3的纵坐标
 ,
,当x=4时,P4的纵坐标
 ,
,当x=5时,P5的纵坐标
 ,
,…
则S1=1×(2-1)=2-1;
S2=1×(1-
 )=1-
)=1- ;
;S3=1×(
 -
- )=
)= -
- ;
;S4=1×(
 -
- )=
)= -
- ;
;…
Sn=
 -
-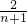 ;
;S1+S2+S3+…+Sn=2-1+1-
 +
+ -
- +
+ -
- +…+
+…+ -
-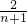 =2-
=2-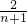 =
= .
.故答案为:
 .
.点评:此题考查了反比例函数图象上点的坐标特征,根据坐标求出个阴影的面积表达式是解题的关键.

练习册系列答案
相关题目
 如图,在反比例函数
如图,在反比例函数 ,S2,…,Sn,则Sn=
,S2,…,Sn,则Sn=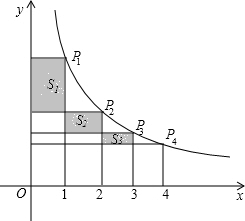 如图,在反比例函数y=
如图,在反比例函数y= n,求:
n,求: (2012•瑞安市模拟)如图,在反比例函数
(2012•瑞安市模拟)如图,在反比例函数