题目内容
如图,在反比例函数y=| 2 | x |
 n,求:
n,求:(1)s1的值;
(2)s6的值;
(3)s1+s2+s3+…+sn的值.(用含n的代数式来表示)
分析:(1)由图可得出P1,P2的坐标,即可求得s1的值;
解答(2)(3)两问时求出Sn=
-
即可解答.
解答(2)(3)两问时求出Sn=
| 2 |
| n |
| 2 |
| n+1 |
解答:解:(1)由题可得P1(1,2),P2(2,1)
所以S1=1×(2-1)=1;
(2)由题知P5(5,
),P6(6,
),P7(7,
)
S6=(6-5)×(
-
)=
;
(3)由题意可以得出Sn=(n-n+1)×(
-
)=
-
所以S1+S2+S3+…+Sn=2(1-
+
-
+…+
-
)=
.
所以S1=1×(2-1)=1;
(2)由题知P5(5,
| 2 |
| 5 |
| 1 |
| 3 |
| 2 |
| 7 |
S6=(6-5)×(
| 1 |
| 3 |
| 2 |
| 7 |
| 1 |
| 21 |
(3)由题意可以得出Sn=(n-n+1)×(
| 2 |
| n |
| 2 |
| n+1 |
| 2 |
| n |
| 2 |
| n+1 |
所以S1+S2+S3+…+Sn=2(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 2n |
| n+1 |
点评:本题考查对反比例函数图象的识别和求解能力.要由图象找出其中隐含的规律.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 如图,在反比例函数
如图,在反比例函数 ,S2,…,Sn,则Sn=
,S2,…,Sn,则Sn=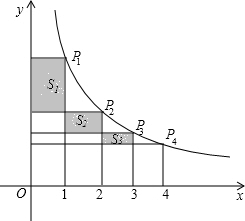 如图,在反比例函数y=
如图,在反比例函数y= (2012•瑞安市模拟)如图,在反比例函数
(2012•瑞安市模拟)如图,在反比例函数