题目内容
 (2012•宁夏)在矩形ABCD中,AB=2,AD=3,P是BC上的任意一点(P与B、C不重合),过点P作AP⊥PE,垂足为P,PE交CD于点E.
(2012•宁夏)在矩形ABCD中,AB=2,AD=3,P是BC上的任意一点(P与B、C不重合),过点P作AP⊥PE,垂足为P,PE交CD于点E.(1)连接AE,当△APE与△ADE全等时,求BP的长;
(2)若设BP为x,CE为y,试确定y与x的函数关系式.当x取何值时,y的值最大?最大值是多少?
(3)若PE∥BD,试求出此时BP的长.
分析:(1)根据全等三角形的对应边相等知AP=AD=3;然后在Rt△ABP中利用勾股定理可以求得BP的长度;
(2)根据相似三角形Rt△ABP∽Rt△PCE的对应边成比例列出关于x、y的方程,通过二次函数的最值的求法来求y的最大值;
(3)如图,连接BD.利用(2)中的函数关系式设BP=x,则CE=-
x2+
x,然后根据相似三角形△CPE∽△CBD的对应边成比例列出关于x的一元二次方程,通过解该方程即可求得此时BP的长度.
(2)根据相似三角形Rt△ABP∽Rt△PCE的对应边成比例列出关于x、y的方程,通过二次函数的最值的求法来求y的最大值;
(3)如图,连接BD.利用(2)中的函数关系式设BP=x,则CE=-
| 1 |
| 2 |
| 3 |
| 2 |
解答: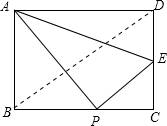 解:(1)∵△APE≌△ADE(已知),AD=3(已知),
解:(1)∵△APE≌△ADE(已知),AD=3(已知),
∴AP=AD=3(全等三角形的对应边相等);
在Rt△ABP中,BP=
=
=
(勾股定理);
(2)∵AP⊥PE(已知),
∴∠APB+∠CPE=∠CPE+∠PEC=90°,
∴∠APB=∠PEC,
又∵∠B=∠C=90°,
∴Rt△ABP∽Rt△PCE,
∴
=
即
=
(相似三角形的对应边成比例),
∴y=-
x2+
x=-
(x-
)2+
∴当x=
时,y有最大值,最大值是
;
(3)如图,连接BD.设BP=x,CE=-
x2+
x
∵PE∥BD,
∴△CPE∽△CBD,
∴
=
(相似三角形的对应边成比例),
即
=
化简得,3x2-13x+12=0
解得,x1=
,x2=3(不合题意,舍去),
∴BP=
.
 解:(1)∵△APE≌△ADE(已知),AD=3(已知),
解:(1)∵△APE≌△ADE(已知),AD=3(已知),∴AP=AD=3(全等三角形的对应边相等);
在Rt△ABP中,BP=
| AP2-AB2 |
| 32-22 |
| 5 |
(2)∵AP⊥PE(已知),
∴∠APB+∠CPE=∠CPE+∠PEC=90°,
∴∠APB=∠PEC,
又∵∠B=∠C=90°,
∴Rt△ABP∽Rt△PCE,
∴
| AB |
| PC |
| BP |
| CE |
| 2 |
| 3-x |
| x |
| y |
∴y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 8 |
∴当x=
| 3 |
| 2 |
| 9 |
| 8 |
(3)如图,连接BD.设BP=x,CE=-
| 1 |
| 2 |
| 3 |
| 2 |
∵PE∥BD,
∴△CPE∽△CBD,
∴
| CP |
| CB |
| CE |
| CD |
即
| 3-x |
| 3 |
-
| ||||
| 2 |
化简得,3x2-13x+12=0
解得,x1=
| 4 |
| 3 |
∴BP=
| 4 |
| 3 |
点评:本题综合考查了矩形的性质、勾股定理、二次函数的最值等知识点.本题中求二次函数的最值时,采用了配方法.

练习册系列答案
相关题目
 (2012•宁夏)如图,C岛在A岛的北偏东45°方向,在B岛的北偏西25°方向,则从C岛看A、B两岛的视角∠ACB=
(2012•宁夏)如图,C岛在A岛的北偏东45°方向,在B岛的北偏西25°方向,则从C岛看A、B两岛的视角∠ACB=
 (2012•宁夏)在⊙O中,直径AB⊥CD于点E,连接CO并延长交AD于点F,且CF⊥AD.求∠D的度数.
(2012•宁夏)在⊙O中,直径AB⊥CD于点E,连接CO并延长交AD于点F,且CF⊥AD.求∠D的度数.