Question

（2012•宁夏）在⊙O中，直径AB⊥CD于点E，连接CO并延长交AD于点F，且CF⊥AD．求∠D的度数．

Answer 1

分析：连接BD，根据平行线的性质可得：BD∥CF，则∠BDC=∠C，根据圆周角定理可得∠BDC=

1

2

∠BOC，则∠C=

1

2

∠BOC，根据直角三角形的两个锐角互余即可求解．

解答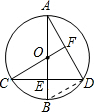：解：方法一：连接BD．        
∵AB是⊙O直径，
∴BD⊥AD．
又∵CF⊥AD，
∴BD∥CF，
∴∠BDC=∠C．
又∵∠BDC=

1

2

∠BOC，
∴∠C=

1

2

∠BOC．
∵AB⊥CD，
∴∠C=30°，
∴∠ADC=60°．
方法二：设∠D=x，
∵CF⊥AD，AB⊥CD，∠A=∠A，
∴△AFO∽△AED，
∴∠D=∠AOF=x，
∴∠AOC=2∠ADC=2x，
∴x+2x=180，
∴x=60，
∴∠ADC=60°．

点评：本题考查了圆周角定理以及直角三角形的性质，正确得到∠C=

1

2

∠BOC是解题的关键．