题目内容
 反比例函数y=
反比例函数y=| k |
| x |
| A、8 | B、4 | C、-8 | D、-4 |
考点:反比例函数系数k的几何意义
专题:
分析:设E的坐标是(m,n),k=mn,则B的坐标是(2m,n),求得D的坐标,然后根据三角形的面积公式求得mn的值,即k的值.
解答:解:设E的坐标是(m,n),k=mn,
则B的坐标是(2m,n),
在y=
中,令x=2m,解得:y=
,
∵S△DBE=1,
∴
|m|•|n-
|=1,即-
×m×
=1,
∴mn=-4.
∴k=-4.
故选D.
则B的坐标是(2m,n),
在y=
| mn |
| x |
| n |
| 2 |
∵S△DBE=1,
∴
| 1 |
| 2 |
| n |
| 2 |
| 1 |
| 2 |
| n |
| 2 |
∴mn=-4.
∴k=-4.
故选D.
点评:本题考查了待定系数法求函数的解析式,利用mn表示出三角形的面积是关键.

练习册系列答案
相关题目
下列等式中:
(1)(a+b)2=a2+b2;
(2)(x-a)(x+b)=x2-(a+b)x-ab;
(3)2a2•2a-1=a;
(4)2a3÷(2a3-a2)=1-2a.
其中不成立的有( )
(1)(a+b)2=a2+b2;
(2)(x-a)(x+b)=x2-(a+b)x-ab;
(3)2a2•2a-1=a;
(4)2a3÷(2a3-a2)=1-2a.
其中不成立的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
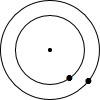 如图,有2个同心圆,半径分别为R和r(单位:厘米),且R>r>1,记两圆之间的圆环面积为P;若把R和r都增加1厘米,记两圆之间的圆环面积为Q,则( )
如图,有2个同心圆,半径分别为R和r(单位:厘米),且R>r>1,记两圆之间的圆环面积为P;若把R和r都增加1厘米,记两圆之间的圆环面积为Q,则( )A、0<
| ||
B、1<
| ||
C、2<
| ||
D、3<
|
设边长为2的正方形的对角线长为a,下列关于a的四种说法:
①
是分数;②a可以用数轴上的一个点来表示;③3<a<4;④a是8的算术平方根.
其中所有正确说法的序号是( )
①
| a |
| 4 |
其中所有正确说法的序号是( )
| A、①④ | B、②④ | C、①②④ | D、①③ |




