题目内容
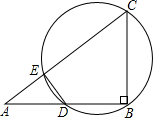
如图,在△ABC的外接圆O中,D是 的中点,AD交BC于点E,连接BD.
的中点,AD交BC于点E,连接BD.(1)列出图中所有相似三角形;
(2)连接DC,若在
 上任取一点K(点A,B,C除外),连接CK,DK,DK交BC于点F,DC2=DF•DK是否成立?若成立,给出证明;若不成立,举例说明.
上任取一点K(点A,B,C除外),连接CK,DK,DK交BC于点F,DC2=DF•DK是否成立?若成立,给出证明;若不成立,举例说明.
【答案】分析:(1)根据相似三角形的判定可以得到相似三角形共有三对;
(2)先根据已知作图,通过证明△KDC∽△CDF,再根据相似三角形的对应边成比例即可得到DC2=DF•DK.
解答: 解:(1)△BDE∽△CAE,△DBE∽△DAB,△ABD∽△AEC.
解:(1)△BDE∽△CAE,△DBE∽△DAB,△ABD∽△AEC.
(2)DC2=DF•DK成立.
证明:∵D是 的中点,
的中点,
∴ =
= ,
,
∴∠DBC=∠DCB(等弧的圆周角相等),
又∵∠DBC=∠DKC,
∴∠DCB=∠DKC,
又∵∠KDC=∠CDF,
∴△KDC∽△CDF,
∴ ,
,
∴DC2=DF•DK.
点评:考查了相似三角形的判定方法及三角形外接圆与外心等知识的掌握情况.
(2)先根据已知作图,通过证明△KDC∽△CDF,再根据相似三角形的对应边成比例即可得到DC2=DF•DK.
解答:
 解:(1)△BDE∽△CAE,△DBE∽△DAB,△ABD∽△AEC.
解:(1)△BDE∽△CAE,△DBE∽△DAB,△ABD∽△AEC.(2)DC2=DF•DK成立.
证明:∵D是
 的中点,
的中点,∴
 =
= ,
,∴∠DBC=∠DCB(等弧的圆周角相等),
又∵∠DBC=∠DKC,
∴∠DCB=∠DKC,
又∵∠KDC=∠CDF,
∴△KDC∽△CDF,
∴
 ,
,∴DC2=DF•DK.
点评:考查了相似三角形的判定方法及三角形外接圆与外心等知识的掌握情况.

练习册系列答案
相关题目
 (在下面的(I)(II)两题中选做一题,若两题都做,按第(I)题评分)
(在下面的(I)(II)两题中选做一题,若两题都做,按第(I)题评分)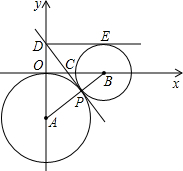 上,过P点作两圆的公切线DP交y轴于D,交x轴于C,
上,过P点作两圆的公切线DP交y轴于D,交x轴于C,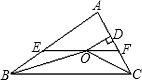 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°+
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°+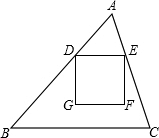 如图,在△ABC中,BC=12,AB=10,sinB=
如图,在△ABC中,BC=12,AB=10,sinB= 如图,在△ABC中,AB=AC,∠BAC=30°,分别以AB、AC为边向形外作两个等腰直角三角形ABD和ACE,使∠BAD=∠CAE=90°.
如图,在△ABC中,AB=AC,∠BAC=30°,分别以AB、AC为边向形外作两个等腰直角三角形ABD和ACE,使∠BAD=∠CAE=90°. 如图,自△ABC的外接圆弧BC上的任一点M,作MD⊥BC于D,P是AM上一点,作PE⊥AC,PF⊥AB,PG⊥BC,E,F,G分别在AC,AB,AD上.证明:E,F,G三点共线.
如图,自△ABC的外接圆弧BC上的任一点M,作MD⊥BC于D,P是AM上一点,作PE⊥AC,PF⊥AB,PG⊥BC,E,F,G分别在AC,AB,AD上.证明:E,F,G三点共线.