题目内容
如图，在矩形ABCD中，AF=DE．BE与CF相等吗？如果相等请说明理由．考点：矩形的性质,全等三角形的判定与性质
专题：
分析：只要证出△ABE≌△DCF就可以了，由于四边形ABCD是矩形，所以已经具备两个条件，再利用已知条件AE=DE，等量加等量和相等，可以得到另外一个条件，利用SAS可证三角形全等．
解答：解：BE与CF相等，
理由如下：
∵四边形ABCD是矩形，
∴∠A=∠D=90°，AB=DC．
∵AF=DE，
∴AE=DF，
在△BAE和△CDF中，
，
∴△BAE≌△CDFSAS），
∴BE=CF．
理由如下：
∵四边形ABCD是矩形，
∴∠A=∠D=90°，AB=DC．
∵AF=DE，
∴AE=DF，
在△BAE和△CDF中，
|
∴△BAE≌△CDFSAS），
∴BE=CF．
点评：本题考查了矩形的性质、全等三角形的判定和性质，题目比较简单，是中考常见题型．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
不等式-x＞3的解集是（ ）
| A、x＜-3 | B、x＞-3 |
| C、x＜3 | D、x＞3 |
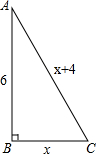求如图的Rt△ABC的面积．