题目内容
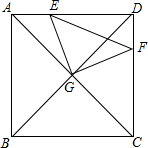 如图,正方形ABCD中,AE=DF=4,△AEG与△DEF的面积比为2:3,那么△EFG的面积是多少?
如图,正方形ABCD中,AE=DF=4,△AEG与△DEF的面积比为2:3,那么△EFG的面积是多少?考点:正方形的性质
专题:
分析:根据正方形的性质可得AG=DG,∠EAG=∠FDG=45°,然后利用“边角边”证明△AEG和△DFG全等,根据全等三角形对应边相等可得EG=FG,∠AGE=∠DGF,再求出∠EGF=∠AGD=90°,从而判断出△EFG是等腰直角三角形,过点G作GH⊥AD于H,根据正方形的性质可得GH=AH=
AD,然后根据等底的三角形的面积的比等于高的比列式求出AD,再求出EH,GH,然后利用勾股定理列式求出EG2,再根据三角形的面积解答即可.
| 1 |
| 2 |
解答:解:在正方形ABCD中,AG=DG,∠EAG=∠FDG=45°,
在△AEG和△DFG中,
,
∴△AEG≌△DFG(SAS),
∴EG=FG,∠AGE=∠DGF,
∴∠EGF=∠DGF+∠DAE=∠EAG+∠DGE=∠AGD=90°,
∴△EFG是等腰直角三角形,
过点G作GH⊥AD于H,
∵四边形ABCD是正方形,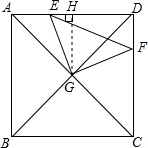
∴GH=AH=
AD,
∵△AEG与△DEF的面积比为2:3,AE=DF,
∴
=
,
∴
=
,
解得AD=16,
∴GH=AH=
×16=8,
EH=AH-AE=8-4=4,
在Rt△EHG中,EG2=EH2+GH2=42+82=80,
∴△EFG的面积=
EG2=
×80=40.
在△AEG和△DFG中,
|
∴△AEG≌△DFG(SAS),
∴EG=FG,∠AGE=∠DGF,
∴∠EGF=∠DGF+∠DAE=∠EAG+∠DGE=∠AGD=90°,
∴△EFG是等腰直角三角形,
过点G作GH⊥AD于H,
∵四边形ABCD是正方形,

∴GH=AH=
| 1 |
| 2 |
∵△AEG与△DEF的面积比为2:3,AE=DF,
∴
| GH |
| DE |
| 2 |
| 3 |
∴
| ||
| AD-4 |
| 2 |
| 3 |
解得AD=16,
∴GH=AH=
| 1 |
| 2 |
EH=AH-AE=8-4=4,
在Rt△EHG中,EG2=EH2+GH2=42+82=80,
∴△EFG的面积=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了正方形的性质,全等三角形的判定与性质,勾股定理,等腰直角三角形的判定与性质,利用等底的三角形的面积的比等于高的比求出正方形的边长AD是解题的关键.

练习册系列答案
相关题目
 如图,将?ABCD纸片折叠,使得B与D重合,EF为折痕.
如图,将?ABCD纸片折叠,使得B与D重合,EF为折痕.  如图,矩形ABCD中,AB=
如图,矩形ABCD中,AB=