题目内容
 如图,AD、CE是钝角△ABC的高,且AD=3,CE=2,AB=4.则BC=
如图,AD、CE是钝角△ABC的高,且AD=3,CE=2,AB=4.则BC=| 8 |
| 3 |
| 8 |
| 3 |
分析:先根据AD、CE是钝角△ABC的高,得出S△ABC=
AB•CE=
BC•AD,再进行整理得出AB•CE=BC•AD,最后把AD=3,CE=2,AB=4代入即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵AD、CE是钝角△ABC的高,
∴S△ABC=
AB•CE=
BC•AD,
∴AB•CE=BC•AD,
∵AD=3,CE=2,AB=4,
∴4×2=BC×3,
∴BC=
;
故答案为:
.
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴AB•CE=BC•AD,
∵AD=3,CE=2,AB=4,
∴4×2=BC×3,
∴BC=
| 8 |
| 3 |
故答案为:
| 8 |
| 3 |
点评:此题考查了三角形的面积,用到的知识点是三角形的面积公式,根据题意得出AB•CE=BC•AD是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 如图:AD、CE是△ABC的中线,AD、CE相交于F,若CE=8厘米,则CF=
如图:AD、CE是△ABC的中线,AD、CE相交于F,若CE=8厘米,则CF=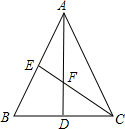 如图,AD、CE是△ABC的角平分线,AD、CE相交于点F,已知∠B=60°,则下列说法中正确的个数是( )
如图,AD、CE是△ABC的角平分线,AD、CE相交于点F,已知∠B=60°,则下列说法中正确的个数是( ) 如图,AD、CE是△ABC的两条高,已知AD=10,CE=9,AB=12.
如图,AD、CE是△ABC的两条高,已知AD=10,CE=9,AB=12. 如图,AD、CE是钝角△ABC的高,且AD=3,CE=2,AB=4.则BC=________.
如图,AD、CE是钝角△ABC的高,且AD=3,CE=2,AB=4.则BC=________.