题目内容
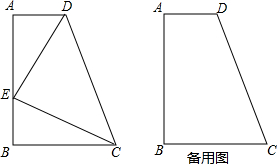 如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=3,BC=4,点E在AB边上,BE=3,∠CED=90°.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=3,BC=4,点E在AB边上,BE=3,∠CED=90°.(1)求CE的长度;
(2)求证:△ADE≌△BEC;
(3)设点P是线段AB上的一个动点,求DP+CP的最小值是多少?
考点:全等三角形的判定与性质,勾股定理,轴对称-最短路线问题
专题:
分析:(1))由∠B=90°,BC=4,BE=3,根据勾股定理求出CE;
(2)先证出∠DEA=∠ECB,即可证明△ADE≌△BEC;
(3)作点D关于AB的对称点F,连接CF交AB于点P,再用勾股定理求出CF的长即为DP+CP的最小值.
(2)先证出∠DEA=∠ECB,即可证明△ADE≌△BEC;
(3)作点D关于AB的对称点F,连接CF交AB于点P,再用勾股定理求出CF的长即为DP+CP的最小值.
解答:解:(1)∵∠B=90°,BC=4,BE=3,
根据勾股定理可得:CE=
=
=5;
(2)∵∠CED=90°,
∴∠CEB+∠DEA=90°,
∵∠B=90°,
∴∠CEB+∠ECB=90°,
∴∠DEA=∠ECB,
∵AD∥BC,∠B=90°,
∴∠A=∠B=90°,
在△ADE和△BEC中,
∴△ADE≌△BEC(AAS);
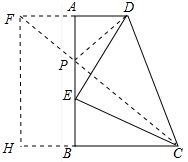 (3)延长DA至F,使得AD=AF,并连接CF,此时CF与AB的交点为点P,连接PD;
(3)延长DA至F,使得AD=AF,并连接CF,此时CF与AB的交点为点P,连接PD;
∵AB⊥AD,且AD=AF,
∴△DFP是等腰三角形,
∴DP=FP,
∴DP+CP的最小值为CF,
过点F作FH垂直CB的长线,垂足为H,如图所示:
根据题意得:CH=7,FH=7,
根据勾股定理可得,CF=
=7
,
即DP+CP的最小值为7
.
根据勾股定理可得:CE=
| BC2+BE2 |
| 42+32 |
(2)∵∠CED=90°,
∴∠CEB+∠DEA=90°,
∵∠B=90°,
∴∠CEB+∠ECB=90°,
∴∠DEA=∠ECB,
∵AD∥BC,∠B=90°,
∴∠A=∠B=90°,
在△ADE和△BEC中,
|
∴△ADE≌△BEC(AAS);
 (3)延长DA至F,使得AD=AF,并连接CF,此时CF与AB的交点为点P,连接PD;
(3)延长DA至F,使得AD=AF,并连接CF,此时CF与AB的交点为点P,连接PD;∵AB⊥AD,且AD=AF,
∴△DFP是等腰三角形,
∴DP=FP,
∴DP+CP的最小值为CF,
过点F作FH垂直CB的长线,垂足为H,如图所示:
根据题意得:CH=7,FH=7,
根据勾股定理可得,CF=
| 72+72 |
| 2 |
即DP+CP的最小值为7
| 2 |
点评:本题考查了勾股定理、轴对称以及最短路线问题;熟练掌握勾股定理和最短路线的作图是解决问题的关键.

练习册系列答案
相关题目
抛物线y=x2+3x-4与x轴交点的个数为( )
| A、1个 | B、2个 | C、0个 | D、3个 |
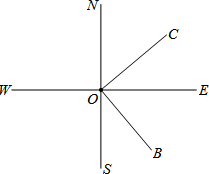 如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余.
如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余. 如图是某个几何体的表面展开图,那么这个几何体是
如图是某个几何体的表面展开图,那么这个几何体是 如图,已知点A、D、C、F在同一条直线上,AB=DE,∠B=∠E,要使△ABC≌△DEF,还需要添加一个条件是
如图,已知点A、D、C、F在同一条直线上,AB=DE,∠B=∠E,要使△ABC≌△DEF,还需要添加一个条件是 如图,将一副直角三角板放在一起,使直角顶点重合于点O.
如图,将一副直角三角板放在一起,使直角顶点重合于点O.