题目内容
如图，△ABC中，D点是边BC的中点，E点在AD上，AE：ED=1：2，BE的延长线与AC相交于F，求AF：FC的值．考点：平行线分线段成比例
专题：
分析：因为D为BC的中点，所以过点D作DG∥EF，交AC于点G，可得AE：ED=AF：FG=1：2，D为中点可得CD：DB=CG：GF=1：1，进一步可求出AF：FC．
解答：解：
过点D作DG∥EF，交AC于点G，
可得AE：ED=AF：FG=1：2，所以FG=2AF，
又D为中点可得CD：DB=CG：GF=1：1，所以CG=GF=2AF，
所以AF：FC=AF：4AF=1：4．
过点D作DG∥EF，交AC于点G，
可得AE：ED=AF：FG=1：2，所以FG=2AF，
又D为中点可得CD：DB=CG：GF=1：1，所以CG=GF=2AF，
所以AF：FC=AF：4AF=1：4．
点评：本题主要考查平行线分线段成比例性质上的运用，解题的关键是找到AF和FC之间的关键．
练习册系列答案
相关题目
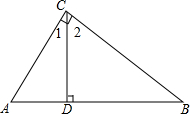如图，Rt△ABC中，∠ACB=90°，CD是AB边上的高，写出分别与∠1，∠2相等的角，并说明理由．
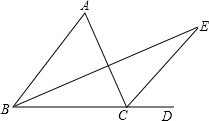如图，在△ABC中，D是BC延长线上的一点，∠ABC，∠ACD的角平分线交于点E．求证：∠E=