Question

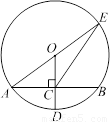
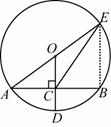
如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．若AB=8，CD=2，求EC的长．

 

 

Answer 1

【答案】

.

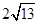【解析】

试题分析：先根据垂径定理求出AC的长,设的⊙O半径x,则OC=x-2,由勾股定理即可得出x的值,故可得出AE的长,连接BE,由圆周角定理可知∠ABE=90º,在Rt△BCE中,根据勾股定理即可求出CE的长.

试题解析：

∵OD⊥AB，

∴AC=BC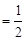AB．

设AO=x．

在Rt△ACO中，AO²=AC²+OC²．

∴x²=4²+(x-2)²．

解得x=5．

∴AE=10，OC=3．

连结BE．

∵AE是直径，

∴∠ABE=90°．

由OC是△ABE的中位线可求BE=2OC=6．

在Rt△CBE中，CE²=BC²+BE²．

∴．

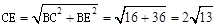考点：1.垂径定理；2.圆周角定理；3.勾股定理.