题目内容
如图,抛物线 (
( )与
)与 轴相交于
轴相交于 两点,点
两点,点 是抛物线的顶点,以
是抛物线的顶点,以 为直径作圆
为直径作圆 交
交 轴于
轴于 两点,
两点, .
.
(1). (3分) 用含 的代数式表示圆
的代数式表示圆 的半径
的半径 的长;
的长;
)
(2). (3分)连结 ,求线段
,求线段 的长;
的长;
(3). (4分)点 是抛物线对称轴正半轴上的一点,且满足以
是抛物线对称轴正半轴上的一点,且满足以 点为圆心的圆
点为圆心的圆 与直线
与直线 和圆
和圆 都相切,求点
都相切,求点 的坐标.
的坐标.
)
解:(1) ,
,  ……………(1分)
……………(1分)
 …(2分)
…(2分) …(3分
…(3分
 ,AB是直径,
,AB是直径,
 , 连结GE,
, 连结GE, …(4分)解,得
…(4分)解,得 …(5分)
…(5分) ,
,
 ,
, …(6分)
…(6分)
设⊙P的半径为 ,P点的坐标为
,P点的坐标为 ,…………………(7分)
,…………………(7分)
由题意可知,当 时,不符合题意,所以
时,不符合题意,所以 .
.
因为⊙P与直线AH相切,过点P作 ,垂足为点M,
,垂足为点M,
 ,…………………(8分)
,…………………(8分)
①当⊙P与⊙G内切时, ∴
∴ ………(9分)
………(9分)
②当⊙P与⊙G外切,

所以满足条件的P点有: ,
,  .…………………(10分
.…………………(10分
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的半径
的半径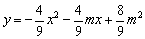 (
( )与
)与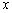 轴相交于
轴相交于 两点,点
两点,点 是抛物线的顶点,以
是抛物线的顶点,以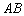 为直径作圆
为直径作圆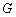 交
交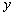 轴于
轴于 两点,
两点, .
.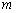 的代数式表示圆
的代数式表示圆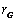 的长;
的长; ,求线段
,求线段 是抛物线对称轴正半轴上的一点,且满足以
是抛物线对称轴正半轴上的一点,且满足以 (
( )与
)与 轴相交于
轴相交于 两点,点
两点,点 是抛物线的顶点,以
是抛物线的顶点,以 为直径作圆
为直径作圆 交
交 轴于
轴于 两点,
两点, .
. 的代数式表示圆
的代数式表示圆 的长;
的长;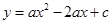 (
( )与
)与 轴交于点
轴交于点 ( 0,4) ,与
( 0,4) ,与 轴交于点
轴交于点 ,
, ,点
,点
 是线段
是线段 上的动点,过点
上的动点,过点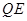 ∥
∥ ,交
,交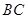 于点
于点 ,连接
,连接 . 当
. 当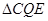 的面积最大时,求点
的面积最大时,求点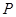 ,与直线
,与直线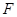 ,点
,点 的坐标为(2,0). 问: 是否存在这样的直线,使得
的坐标为(2,0). 问: 是否存在这样的直线,使得 是等腰三角形?若存在,请求出点
是等腰三角形?若存在,请求出点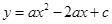 (
(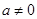 )与
)与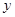 轴交于点
轴交于点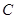 ( 0,4) ,与
( 0,4) ,与 轴交于点
轴交于点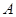 ,
,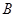 ,点
,点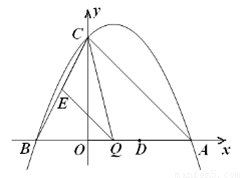
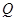 是线段
是线段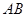 上的动点,过点
上的动点,过点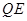 ∥
∥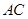 ,交
,交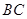 于点
于点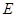 ,连接
,连接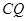 . 当
. 当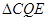 的面积最大时,求点
的面积最大时,求点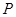 ,与直线
,与直线 ,点
,点 的坐标为(2,0). 问: 是否存在这样的直线,使得
的坐标为(2,0). 问: 是否存在这样的直线,使得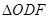 是等腰三角形?若存在,请求出点
是等腰三角形?若存在,请求出点