题目内容
9. 如图,在Rt△ABC中,∠ACB=90°,AC=5cm,AB=13cm,将△ABC绕点B顺时针旋转60°,得到△EBD,连接DC,则△BCD的周长为36cm.
如图,在Rt△ABC中,∠ACB=90°,AC=5cm,AB=13cm,将△ABC绕点B顺时针旋转60°,得到△EBD,连接DC,则△BCD的周长为36cm.
分析 在△ABC中,依据勾股定理可求得BC的长,然后依据旋转的性质可证明△BCD为等边三角形,故此可求得△BCD的周长.
解答 解:∵△ABC绕点B顺时针旋转60°,得到△BDE,
∴∠CBD=60°,BC=BD,
∴△BCD为等边三角形.
在Rt△ABC中,∠ACB=90°,AC=5cm,AB=13cm,
∴CB=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12cm.
∴△BCD的周长=12×3=36cm.
点评 本题考查了旋转的性质,勾股定理的应用,证得△BCD为等边三角形是解题的关键.

练习册系列答案
相关题目
8.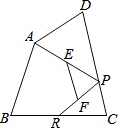 如图,已知四边形ABCD中,R,P分别是BC,CD边上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,下列结论成立的是( )
如图,已知四边形ABCD中,R,P分别是BC,CD边上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,下列结论成立的是( )
 如图,已知四边形ABCD中,R,P分别是BC,CD边上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,下列结论成立的是( )
如图,已知四边形ABCD中,R,P分别是BC,CD边上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,下列结论成立的是( )| A. | △EFP的周长不变 | B. | 线段EF的长与点P的位置无关 | ||
| C. | 点P到EF的距离不变 | D. | ∠APR的大小不变 |
20.已知实数x,y满足|x-3|+(y+4)2=0,则代数式(x+y)2017的值为( )
| A. | -1 | B. | 1 | C. | 2012 | D. | -2008 |
4.$\frac{1}{4}$的平方根是( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | ±$\frac{1}{2}$ | D. | ±$\frac{1}{16}$ |
18.小明统计了他家今年3月份打电话的次数及通话时间,并列出了频数分布表:
则通话时间不超过10min的频率为( )
| 通话时间x/min | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 |
| 频数(通话次数) | 20 | 15 | 9 | 6 |
| A. | 0.1 | B. | 0.3 | C. | 0.5 | D. | 0.7 |
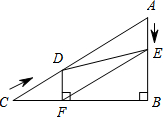 如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts(0<t≤15).过点DDF⊥BC于点F,连接DE,EF.
如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts(0<t≤15).过点DDF⊥BC于点F,连接DE,EF.