题目内容
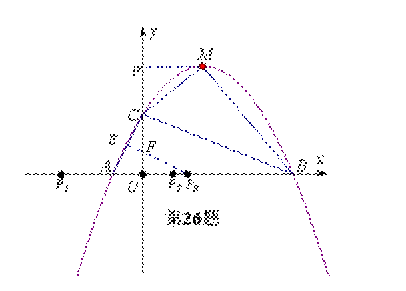
如图,已知抛物线y=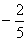 x2+
x2+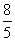 x+2交x轴于A、B两点(点A在点B的左侧),与y轴交于点C。
x+2交x轴于A、B两点(点A在点B的左侧),与y轴交于点C。
(1)求点A、B、C的坐标。
(2)若点M为抛物线的顶点,连接BC、CM、BM,求△BCM的面积。
(3)连接AC,在x轴上是否存在点P使△ACP为等腰三角形,若存在,请求出点P的坐标;若不存在,请说明理由。

解:(1)令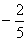 x2+
x2+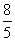 x+2=0,解得
x+2=0,解得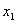 =-1,
=-1,
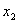 =5……………1分
=5……………1分
令x=0,则y=2,所以A、B、C的坐标分别是A(-1,0)、B(5,0)、C(0,2)……………2分
(2)顶点M的坐标是M(2, )……………3分
)……………3分
过M作MN垂直y轴于N,所以△BCM的面积=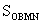 -
-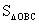 -
- =
=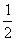 (2+5)×
(2+5)× -
-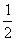 ×5×2-
×5×2-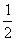 ×(
×( -2)×2=6……………5分
-2)×2=6……………5分
(3)当以AC为腰时,在x轴上有两个点分别为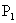 ,
,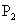 ,易求AC=
,易求AC=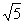 ……………6分
……………6分
则0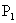 =1+
=1+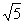 ,O
,O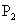 =
=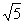 -1,所以
-1,所以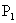 ,
,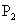 的坐标分别是
的坐标分别是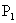 (-1-
(-1-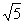 ,0),
,0),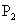 (
(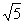 -1,0)
-1,0)
……………7分
当以AC为底时,作AC的垂直平分线交x轴于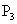 ,交y轴于F,垂足为E,CE=
,交y轴于F,垂足为E,CE=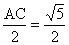
……8分
易证△CEF∽△COA所以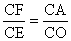 ,而,所以
,而,所以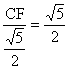 ,CF=
,CF=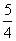
OF=OC-CF=2-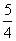 =
=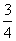 , EF=
, EF=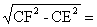
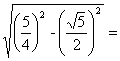
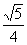 ……………9分
……………9分
又△CEF∽△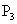 OF,所以,
OF,所以,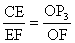 求得O
求得O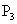 =
=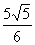
则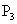 的坐标为
的坐标为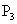 (
(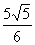 ,0)
,0)
所以存在 、
、 、
、 三点,它们的坐标分别是
三点,它们的坐标分别是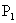 (-1-
(-1-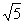 ,0)、
,0)、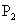 (
(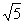 -1,0)、
-1,0)、
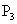 (
(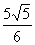 ,0)
,0)

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 ,
, ,
, ,
, ,……满足下列条件:
,……满足下列条件: ,
, ,
, ,……依次类推,则
,……依次类推,则 的值为( )
的值为( ) 07
07  D. -2013
D. -2013
 的图象经过C,求双曲线和直线AB的解析式
的图象经过C,求双曲线和直线AB的解析式
 、2、
、2、 D.5、12、13
D.5、12、13
 有意义,那么字母x的取值范围是( )
有意义,那么字母x的取值范围是( ) ,按相同比例分配到各组,共分成5个组.
,按相同比例分配到各组,共分成5个组.