题目内容
已知:如图所示,在△ABC中,∠C=90°,⊙O内切于△ABC,分别与AB、BC、CA切于点D、E、F.AD=3厘米,BD=2厘米.
求:阴影部分的面积.

答案:
解析:
解析:
|
解:如图所示, 连结OE,OF,∵⊙O内切于△ABC,则OE⊥BC,OF⊥AC, ∵∠C=90°,且OE=OF, ∴四边形OECF是正方形. 设⊙O的半径为r, ∵AF=AD=3,BE=BD=2,∴AC=r+3,BC=r+2. 而AB=3+2=5. 由勾股定理,有(r+3)2+(r+2)2=52, 整理,得r2+5r-6=0, 解得,r1=1,r2=-6(不合题意,舍去). ∴AC=3+1=4,BC=2+1=3, ∴S阴影= 解析:此题的关键是求⊙O的半径长.连结EO、FO,显然四边形OECF是一个正方形,而AF=AD,BE=BD,利用勾股定理可求得⊙O的半径. |

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目

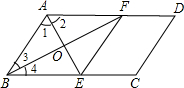 阅读下述说明过程,讨论完成下列问题:
阅读下述说明过程,讨论完成下列问题: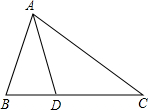 已知:如图所示,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
已知:如图所示,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.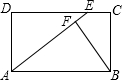 已知:如图所示,在矩形ABCD中,E为DC上的一点,BF⊥AE于点F,且BF=BC,求证:AE=AB.
已知:如图所示,在矩形ABCD中,E为DC上的一点,BF⊥AE于点F,且BF=BC,求证:AE=AB.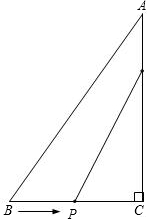 同时出发,其中点P以1厘米/秒的速度沿着线段BC向点C运动,点Q以2厘米/秒的速度沿着线段CA向点A运动.
同时出发,其中点P以1厘米/秒的速度沿着线段BC向点C运动,点Q以2厘米/秒的速度沿着线段CA向点A运动. 点M,连接DC.
点M,连接DC.