题目内容
已知:如图所示,在平面直角坐标系中,函数y=| m | x |
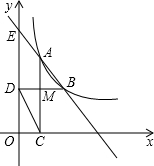 点M,连接DC.
点M,连接DC.(1)求m的值;
(2)求证:四边形ACDE为平行四边形;
(3)若AB=CD,求直线AB的函数解析式.
分析:(1)直接将A的值代入函数 y=
中,即可得出k的值,便可得出解析式;
(2)通过求点E的坐标求得线段OE的长等于ED的长,然后利用对边平行且相等的四边形为平行四边形来判定平行四边形.
(3)利用证得的平行四边形的性质证得AE为中位线求得点B的坐标,然后用待定系数法确定一次函数的解析式.
| k |
| x |
(2)通过求点E的坐标求得线段OE的长等于ED的长,然后利用对边平行且相等的四边形为平行四边形来判定平行四边形.
(3)利用证得的平行四边形的性质证得AE为中位线求得点B的坐标,然后用待定系数法确定一次函数的解析式.
解答:解:(1)∵函数y=
经过点A(1,4),
∴4=
(1分),
∴m=4,
(2)设直线AB的解析式为y=kx+n,
∵直线AB经过点A(1,4),B(a,b),(2分)
∴
,
解得:k=
,n=
,
∴y=
x+
(3分),
∴E(0,
),即OE=
,
又∵BD⊥y轴,
∴OD=b(4分)
∴ED=
-b=
,
又∵点B(a,b)在函数y=
上,
∴ab=m=4(5分),
∴ED=
=
=4,
又∵AC⊥x轴,
∴AC=4(6分),
∴AC∥ED,AC=ED,
∴四边形ACDE为平行四边形;
(3)∵四边形ACDE为平行四边形,
∴AE=CD,
又∵AB=CD(7分),
∴AE=AB,
过点A作AF⊥y轴,则AF∥DB,AF=1,
∴AF为△EBD的中位线(8分),
BD=2AF=2,即a=2(9分),
∵ab=4,∴b=2,
将a=2,b=2代入y=
x+
中得y=-2x+6,
∴直线AB的函数解析式为y=-2x+6.(10分)
| m |
| x |
∴4=
| m |
| 1 |
∴m=4,
(2)设直线AB的解析式为y=kx+n,
∵直线AB经过点A(1,4),B(a,b),(2分)
∴
|
解得:k=
| b-4 |
| a-1 |
| 4a-b |
| a-1 |
∴y=
| b-4 |
| a-1 |
| 4a-b |
| a-1 |
∴E(0,
| 4a-b |
| a-1 |
| 4a-b |
| a-1 |
又∵BD⊥y轴,
∴OD=b(4分)
∴ED=
| 4a-b |
| a-1 |
| 4a-ab |
| a-1 |
又∵点B(a,b)在函数y=
| m |
| x |
∴ab=m=4(5分),
∴ED=
| 4a-ab |
| a-1 |
| 4a-4 |
| a-1 |
又∵AC⊥x轴,
∴AC=4(6分),
∴AC∥ED,AC=ED,
∴四边形ACDE为平行四边形;
(3)∵四边形ACDE为平行四边形,

∴AE=CD,
又∵AB=CD(7分),
∴AE=AB,
过点A作AF⊥y轴,则AF∥DB,AF=1,
∴AF为△EBD的中位线(8分),
BD=2AF=2,即a=2(9分),
∵ab=4,∴b=2,
将a=2,b=2代入y=
| b-4 |
| a-1 |
| 4a-b |
| a-1 |
∴直线AB的函数解析式为y=-2x+6.(10分)
点评:本题考查了反比例函数的综合知识,其中渗透了平行四边形的判定和性质,是一道难度较大的反比例函数综合题.

练习册系列答案
相关题目
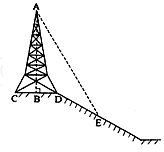
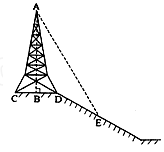
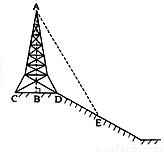
 9、如图所示,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12米,塔影长DE=18米,小明和小华的身高都是1.6米,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2米和1米,那么塔高AB为
9、如图所示,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12米,塔影长DE=18米,小明和小华的身高都是1.6米,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2米和1米,那么塔高AB为