题目内容
14.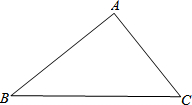 在△ABC中,AB=4,AC=3,BC=5,动点P从点C出发,沿着CB方向运动,速度为每秒3个单位,到达点B时运动停止,设运动时间为t秒,请解答下列问题:
在△ABC中,AB=4,AC=3,BC=5,动点P从点C出发,沿着CB方向运动,速度为每秒3个单位,到达点B时运动停止,设运动时间为t秒,请解答下列问题:(1)求BC上的高;
(2)当t为何值时,△ACP为等腰三角形?
分析 (1)直接利用勾股定的逆定理得出△ABC是直角三角形,进而利用三角形面积得出答案;
(2)分别利用①当AP=AC时,②当AC=CP′时,③当AP″=CP″时,结合锐角三角函数关系得出答案.
解答 解:(1)∵32+42=52,
∴△ABC是直角三角形,
设BC上的高为x,则$\frac{1}{2}$×AB×AC=$\frac{1}{2}$×BC×x,
$\frac{1}{2}×3×4$=$\frac{1}{2}×5$x,
解得:x=2.4,
故BC边上高为2.4;
(2)①当AP=AC时,过A作AD⊥BC,
∵cosC=$\frac{AC}{CB}$=$\frac{3}{5}$,
∴CD=ACcosC=3×$\frac{3}{5}$=$\frac{9}{5}$,
∴CP=$\frac{18}{5}$,
∵P的速度为每秒3个单位,
∴t=$\frac{18}{5}$÷3=$\frac{6}{5}$;
②当AC=CP′时,
∵AC=3,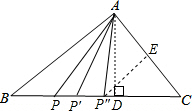
∴CP′=3,
∴t=3÷3=1;
③当AP″=CP″时,
过P″作P″E⊥AC,
∵AC=3,AP″=CP″,
∴EC=1.5,
∵cosC=$\frac{AC}{BC}$=$\frac{3}{5}$
CP″=$\frac{EC}{cosC}$=$\frac{1.5}{\frac{3}{5}}$=2.5,
则t=2.5÷3=$\frac{5}{6}$
综上所述:t=1,$\frac{6}{5}$,$\frac{5}{6}$.
点评 此题主要考查了勾股定定理以及逆定理、锐角三角函数关系,正确利用分类讨论求解是解题关键.

练习册系列答案
相关题目
9.下列说法错误的是( )
| A. | 两个面积相等的圆一定全等 | |
| B. | 全等三角形是指形状、大小都相同的三角形 | |
| C. | 底边相等的两个等腰三角形全等 | |
| D. | 斜边上中线和一条直角边对应相等的两直角三角形全等 |
 如图,OB、OC是⊙O的半径,A是⊙O上的一点,若∠B=30°,∠C=20°,则△BAC=50°.
如图,OB、OC是⊙O的半径,A是⊙O上的一点,若∠B=30°,∠C=20°,则△BAC=50°.