题目内容
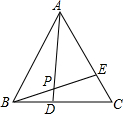 如图,等边△ABC中,BD=CE,AD与BE相交于点P,则∠APB的度数是
如图,等边△ABC中,BD=CE,AD与BE相交于点P,则∠APB的度数是考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:易证△ABD≌△BCE,即可求得∠BAD=∠CBE,根据三角形内角和为180°即可解题.
解答:解:在△ABD和△BCE中,
,
∴△ABD≌△BCE,(SAS)
∴∠BAD=∠CBE,
∵∠APB=180°-∠BAD-∠ABP,
∴∠APB=180°-∠CBP-∠ABP=180°-∠ABC=120°.
故答案为120°.
|
∴△ABD≌△BCE,(SAS)
∴∠BAD=∠CBE,
∵∠APB=180°-∠BAD-∠ABP,
∴∠APB=180°-∠CBP-∠ABP=180°-∠ABC=120°.
故答案为120°.
点评:本题考查了全等三角形的判定和全等三角形对应角相等的性质,本题中求证是解题的关键.

练习册系列答案
相关题目
若(x-5y)(x-by)=x2-3xy+ay2,则a、b的值为( )
| A、a=10,b=-2 |
| B、a=-10,b=-2 |
| C、a=10,b=2 |
| D、a=-10,b=2 |
 如图,图中共有三角形( )
如图,图中共有三角形( )| A、4个 | B、5个 | C、6个 | D、8个 |
在-
,π,-0.1010010001…,0,0.33
这五个数中,有理数的个数为( )
| 22 |
| 7 |
| • |
| 3 |
| A、1 | B、2 | C、3 | D、4 |
下列数据不能确定物体位置的是( )
| A、6楼7号 |
| B、北偏东20° |
| C、龙华路25号 |
| D、东经118°、北纬40° |
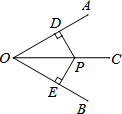 如图,∠AOC=∠BOC,点P在OC上,PD⊥OA于点D,PE⊥OB于点E,若OD=8,OP=10,则PE=
如图,∠AOC=∠BOC,点P在OC上,PD⊥OA于点D,PE⊥OB于点E,若OD=8,OP=10,则PE=