题目内容
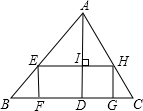如图所示，四边形EFGH是三角形ABC的内接矩形，AD⊥BC，垂足为D，BC=21cm，AD=14cm，EF：FG=1：2，求矩形EFGH的面积．
分析：先设矩形的边长EF=x，利用矩形的性质可知EH∥BC，利用相识三角形判定定理，可得△AEH∽△ABC，再利用相似三角形的性质可得比例线段，可求x，即EF，亦可求得FG，可求出矩形EFGH的面积．
解答：解：如图，设矩形的边长EF=x，则FG=2x，
∵四边形EFGH是三角形ABC的内接矩形，
∴EH∥BC，EH=FG，
∴△AEH∽△ABC，
又∵AD⊥BC，则ID=x，AI=AD-ID，
∴
=
，BC=21cm，AD=14cm，
∴
=
，
解得，x=6cm，即2x=12cm，
∴S矩形EFGH=EF×FG=6×12=72cm2．
答：矩形EFGH的面积为72cm2．
∵四边形EFGH是三角形ABC的内接矩形，
∴EH∥BC，EH=FG，
∴△AEH∽△ABC，
又∵AD⊥BC，则ID=x，AI=AD-ID，
∴
| EH |
| BC |
| AI |
| AD |
∴
| 2x |
| 21 |
| 14-x |
| 14 |
解得，x=6cm，即2x=12cm，
∴S矩形EFGH=EF×FG=6×12=72cm2．
答：矩形EFGH的面积为72cm2．
点评：本题主要考查了矩形的性质和相似三角形的判定与性质，知道相似三角形的对应高之比就等于对应边之比，即相识比．
练习册系列答案
阅读快车系列答案
相关题目
30、如图所示，四边形ABCD是正方形，G是BC上任意一点（点G与D、C不重合），AE⊥DG于E．CF∥AE交DG于F．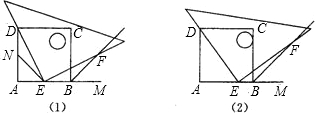
F，进而猜想此时DE与EF有怎样的数量关系．
13、
（Ⅰ）已知：如图，平行四边形ABCD的对角线AC、BD相交于点O，EF过点O与AB、CD分别相交于点E、F．
25、友情提示：本题有A、B两题，请你任选一题作答，A题满分9分，B题满分12分．若两题都做，只能按A题评分．