题目内容
如图所示,四边形ABCD是正方形,M是AB延长线上一点,直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一直角边与∠CBM的平分线BF相交于点F.(1)如图1所示,当点E在AB边的中点位置时:
①通过测量DE,EF的长度,猜想DE与EF满足的数量关系是
②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是
③请证明你的上述两个猜想;
(2)如图2所示,当点E在AB边上的任意位置时,请你在AD边上找到一点N,使得NE=B
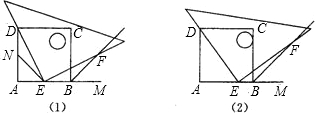 F,进而猜想此时DE与EF有怎样的数量关系.
F,进而猜想此时DE与EF有怎样的数量关系.
分析:根据图形可以得到DE=EF,NE=BF,要证明这两个关系,只要证明△DNE≌△EBF即可.在第二个图形中,只要验证一下这个相等关系是否还成立就可以.
解答:解:(1)①DE=EF;
②NE=BF;
③∵四边形ABCD为正方形,
∴AD=AB,∠DAB=∠ABC=90°,
∵N,E分别为AD,AB中点,
∴AN=DN=
AD,AE=EB=
AB,
∴DN=BE,AN=AE,
∵∠DEF=90°,
∴∠AED+∠FEB=90°,
又∵∠ADE+∠AED=90°,
∴∠FEB=∠ADE,
又∵AN=AE,
∴∠ANE=∠AEN,
又∵∠A=90°,
∴∠ANE=45°,
∴∠DNE=180°-∠ANE=135°,
又∵∠CBM=90°,BF平分∠CBM,
∴∠CBF=45°,∠EBF=135°,
在△DNE和△EBF中
,
∴△DNE≌△EBF(ASA),
∴DE=EF,NE=BF.

(2)在DA上截取DN=EB(或截取AN=AE),
连接NE,则点N可使得NE=BF.
此时DE=EF.
证明方法同(1),证△DNE≌△EBF(ASA).
②NE=BF;
③∵四边形ABCD为正方形,
∴AD=AB,∠DAB=∠ABC=90°,
∵N,E分别为AD,AB中点,
∴AN=DN=
| 1 |
| 2 |
| 1 |
| 2 |
∴DN=BE,AN=AE,
∵∠DEF=90°,
∴∠AED+∠FEB=90°,
又∵∠ADE+∠AED=90°,
∴∠FEB=∠ADE,
又∵AN=AE,
∴∠ANE=∠AEN,
又∵∠A=90°,
∴∠ANE=45°,
∴∠DNE=180°-∠ANE=135°,
又∵∠CBM=90°,BF平分∠CBM,
∴∠CBF=45°,∠EBF=135°,
在△DNE和△EBF中
|
∴△DNE≌△EBF(ASA),
∴DE=EF,NE=BF.

(2)在DA上截取DN=EB(或截取AN=AE),
连接NE,则点N可使得NE=BF.
此时DE=EF.
证明方法同(1),证△DNE≌△EBF(ASA).
点评:此题主要考查了正方形的性质以及全等三角形的判定与性质等知识,解决本题的关键就是求证△DNE≌△EBF.

练习册系列答案
相关题目
 21、如图所示,四边形ABCD是平行四边形,E,F分别在AD,CB的延长线上,且DE=BF,连接FE分别交AB,CD于点H,G.
21、如图所示,四边形ABCD是平行四边形,E,F分别在AD,CB的延长线上,且DE=BF,连接FE分别交AB,CD于点H,G. 12、如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )
12、如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )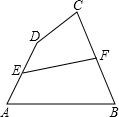 如图所示,四边形ABCD中,E、F分别为AD、BC的中点.
如图所示,四边形ABCD中,E、F分别为AD、BC的中点.
