题目内容
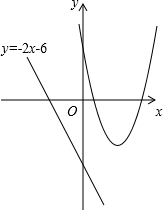 (2013•柳州)已知二次函数y=ax2+bx+c(a≠0)的图象经过点(1,0),(5,0),(3,-4).
(2013•柳州)已知二次函数y=ax2+bx+c(a≠0)的图象经过点(1,0),(5,0),(3,-4). (1)求该二次函数的解析式;
(2)当y>-3,写出x的取值范围;
(3)A、B为直线y=-2x-6上两动点,且距离为2,点C为二次函数图象上的动点,当点C运动到何处时△ABC的面积最小?求出此时点C的坐标及△ABC面积的最小值.
分析:(1)利用待定系数法求出抛物线的解析式;
(2)求出y=3时x的值,结合函数图象,求出y>-3时x的取值范围;
(3)△ABC的底边AB长度为2,是定值,因此当AB边上的高最小时,△ABC的面积最小.如解答图所示,由点C向直线y=-2x-6作垂线,利用三角函数(或相似三角形)求出高CE的表达式,根据表达式求出CE的最小值,这样问题得解.
(2)求出y=3时x的值,结合函数图象,求出y>-3时x的取值范围;
(3)△ABC的底边AB长度为2,是定值,因此当AB边上的高最小时,△ABC的面积最小.如解答图所示,由点C向直线y=-2x-6作垂线,利用三角函数(或相似三角形)求出高CE的表达式,根据表达式求出CE的最小值,这样问题得解.
解答:解:(1)∵点(1,0),(5,0),(3,-4)在抛物线上,
∴
,
解得
.
∴二次函数的解析式为:y=x2-6x+5.
(2)在y=x2-6x+5中,令y=-3,即x2-6x+5=-3,
整理得:x2-6x+8=0,解得x1=2,x2=4.
结合函数图象,可知当y>-3时,x的取值范围是:x<2或x>4.
(3)设直线y=-2x-6与x轴,y轴分别交于点M,点N,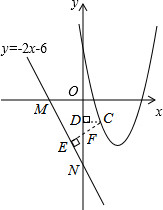
令x=0,得y=-6;令y=0,得x=-3
∴M(-3,0),N(0,-6),
∴OM=3,ON=6,由勾股定理得:MN=3
,
∴tan∠MNO=
=
,sin∠MNO=
=
.
设点C坐标为(x,y),则y=x2-6x+5.
过点C作CD⊥y轴于点D,则CD=x,OD=-y,DN=6+y.
过点C作直线y=-2x-6的垂线,垂足为E,交y轴于点F,
在Rt△CDF中,DF=CD•tan∠MNO=
x,CF=
=
=
=
x.
∴FN=DN-DF=6+y-
x.
在Rt△EFN中,EF=FN•sin∠MNO=
(6+y-
x).
∴CE=CF+EF=
x+
(6+y-
x),
∵C(x,y)在抛物线上,∴y=x2-6x+5,代入上式整理得:
CE=
(x2-4x+11)=
(x-2)2+
,
∴当x=2时,CE有最小值,最小值为
.
当x=2时,y=x2-6x+5=-3,∴C(2,-3).
△ABC的最小面积为:
AB•CE=
×2×
=
.
∴当C点坐标为(2,-3)时,△ABC的面积最小,面积的最小值为
.
∴
|
解得
|
∴二次函数的解析式为:y=x2-6x+5.
(2)在y=x2-6x+5中,令y=-3,即x2-6x+5=-3,
整理得:x2-6x+8=0,解得x1=2,x2=4.
结合函数图象,可知当y>-3时,x的取值范围是:x<2或x>4.
(3)设直线y=-2x-6与x轴,y轴分别交于点M,点N,

令x=0,得y=-6;令y=0,得x=-3
∴M(-3,0),N(0,-6),
∴OM=3,ON=6,由勾股定理得:MN=3
| 5 |
∴tan∠MNO=
| OM |
| ON |
| 1 |
| 2 |
| OM |
| MN |
| ||
| 5 |
设点C坐标为(x,y),则y=x2-6x+5.
过点C作CD⊥y轴于点D,则CD=x,OD=-y,DN=6+y.
过点C作直线y=-2x-6的垂线,垂足为E,交y轴于点F,
在Rt△CDF中,DF=CD•tan∠MNO=
| 1 |
| 2 |
| DF |
| sin∠DCF |
| DF |
| sin∠MNO |
| ||||
|
| ||
| 2 |
∴FN=DN-DF=6+y-
| 1 |
| 2 |
在Rt△EFN中,EF=FN•sin∠MNO=
| ||
| 5 |
| 1 |
| 2 |
∴CE=CF+EF=
| ||
| 2 |
| ||
| 5 |
| 1 |
| 2 |
∵C(x,y)在抛物线上,∴y=x2-6x+5,代入上式整理得:
CE=
| ||
| 5 |
| ||
| 5 |
7
| ||
| 5 |
∴当x=2时,CE有最小值,最小值为
7
| ||
| 5 |
当x=2时,y=x2-6x+5=-3,∴C(2,-3).
△ABC的最小面积为:
| 1 |
| 2 |
| 1 |
| 2 |
7
| ||
| 5 |
7
| ||
| 5 |
∴当C点坐标为(2,-3)时,△ABC的面积最小,面积的最小值为
7
| ||
| 5 |
点评:本题是二次函数综合题型,考查了二次函数的图象与性质、待定系数法、一次函数的图象与性质、解直角三角形(或相似三角形)等知识点.难点在于第(3)问,确定高CE的表达式是解题的关键所在;本问的另一解法是:直线y=-2x+k与抛物线y=x2-6x+5相切时,切点即为所求的点C,同学们可以尝试此思路,以求触类旁通、举一反三.

练习册系列答案
相关题目
 (2013•柳州二模)已知:如图所示的一张矩形纸片ABCD,(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE,若AE=8cm,△ABF的面积为33cm,则△ABF的周长等于( )
(2013•柳州二模)已知:如图所示的一张矩形纸片ABCD,(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE,若AE=8cm,△ABF的面积为33cm,则△ABF的周长等于( ) (2013•柳州二模)已知:如图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0).
(2013•柳州二模)已知:如图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0).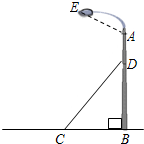 (2013•柳州二模)如图,一个钢结构支柱AB被钢缆CD固定于地面,已知DC=5米,sin∠DCB=
(2013•柳州二模)如图,一个钢结构支柱AB被钢缆CD固定于地面,已知DC=5米,sin∠DCB=