Question

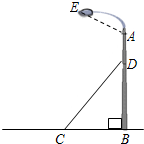（2013•柳州二模）如图，一个钢结构支柱AB被钢缆CD固定于地面，已知DC=5米，sin∠DCB=

3

5

．
（1）求C、B两地距离；
（2）若AD=2米，钢结构的顶端E距离A处2.6米，且∠EAB=120°，则钢结构的顶端E距离地面多少米？

Answer 1

分析：（1）在Rt△DCB中，利用三角函数的定义与勾股定理可求得CB；
（2）过点E作EF⊥AB于点F．由∠EAB=120°，得∠EAF=60°，再根据三角函数求得AF，从而得出答案．

解答：解：（1）在Rt△DCB中，
∵sin∠DCB=

DB

DC

=

3

5

，
设DB=3x，则DC=5x，由勾股定理，得CB=4x，
∵DC=5x=5，
∴x=1．
∴CB=4．
∴C、B两点的距离是4米；

（2）如图，过点E作EF⊥AB于点F．
∵∠EAB=120°，
∴∠EAF=60°，
∴AF=AE•cos∠EAF=2.6×

1

2

=1.3（米），
∴FB=AF+AD+DB=1.3+2+3=6.3（米），
∴钢结构的顶端E距离地面6.3米．

点评：本题考查了解直角三角形的应用，运用三角函数可得出答案，难度适中．