Question

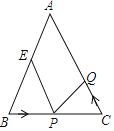
【题目】如图，在△ABC中，∠B＝∠C，AB＝10cm，BC＝8cm，E为AB的中点，点P在线段BC上以3cm/s的速度由点B向点C运动；同时，点Q在线段CA上由点C向点A运动，当点Q的速度为多少时，能够使△BPE和△CQP全等？

Answer 1

【答案】3cm/s或cm/s

【解析】

根据等腰三角形的性质得到∠B＝∠C，设点P、Q的运动时间为t，则BP＝3t，根据线段中点的定义得到BE＝×10＝5cm，PC＝（83t）cm，①当BE，PC是对应边时，②当BD与CQ是对应边时根据全等三角形的性质列方程即可得到结论．

∵AB＝AC，

∴∠B＝∠C，

设点P、Q的运动时间为t，则BP＝3t，

∵AB＝10cm，BC＝8cm，E为AB的中点，

∴BE＝×10＝5cm，PC＝（83t）cm，

①当BE，PC是对应边时，

∵△BPE和△CQP全等，

∴BE＝PC，BP＝CQ，

∴5＝83t，

解得：t＝1，

∴点Q的速度为3cm/s；

②当BD与CQ是对应边时，

∵△BPE和△CQP全等，

∴BD＝CQ，BP＝PC，

∴3t＝83t，

解得：t＝，

∴点Q的速度为，

综上所述，当点Q的速度为3 cm/s或cm/s时，能够使△BPE和△CQP全等．