题目内容
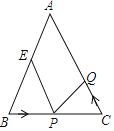
【题目】如图，在Rt△ABC中，
，
角平分线交BC于O，以OB为半径作⊙O.（1）判定直线AC是否是⊙O的切线，并说明理由;
（2）连接AO交⊙O于点E，其延长线交⊙O于点D，
，求
的值;
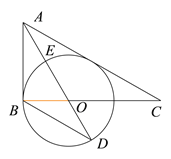
（3）在（2）的条件下，设
的半径为3，求AC的长.
【答案】（1）见解析；（2）
【解析】分析：（1）由于题目没有说明直线AC与⊙O有交点，所以过点O作OF⊥AC于点F，然后证明OB=OF即可；
（2）连接BE，先求证∠ABE=∠ODB，然后可知△ABE∽△ADB，所以
，而tan∠D=
，于是得到结论；
（3）设
在
和中根据
列二元一次方程组求解即可.
详解：（1）AC是⊙O的切线
理由：
，
，
作
于
，
是
的角平分线，
，
AC是⊙O的切线
(2)连接
，
是⊙O的直径，
,即
.
. 
又 
(同角) ，
∽ 
,
(3) 设
在和中，由三角函数定义有：
得：
解之得：
即
的长为
练习册系列答案
相关题目
