题目内容
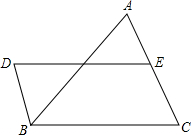
 如图,DB∥AC,且DB=
如图,DB∥AC,且DB=| 1 | 2 |
(1)求证:BC=DE;
(2)连接AD、BE,探究:当△ABC满足什么条件时,四边形DBEA是矩形?并说明理由.
分析:(1)根据中点的定义可得EC=
AC,然后得到DB=EC,然后证明四边形BCED是平行四边形,根据平行四边形的对边相等即可得证;
(2)同(1)的方法可证四边形DBEA是平行四边形,根据等腰三角形三线合一的性质得出∠BEA=90°,根据有一个角是直角的平行四边形是矩形推出即可.
| 1 |
| 2 |
(2)同(1)的方法可证四边形DBEA是平行四边形,根据等腰三角形三线合一的性质得出∠BEA=90°,根据有一个角是直角的平行四边形是矩形推出即可.
解答:(1)证明:∵E是AC的中点,
∴EC=
AC,
∵DB=
AC,
∴DB=EC,
又∵DB∥AC,
∴四边形BCED是平行四边形(一组对边平行且相等的四边形是平行四边形),
∴BC=DE;
(2)解:△ABC满足AB=BC时,四边形DBEA是矩形.
理由如下:∵E是AC的中点,
∴AE=
AC,
∵DB=
AC,
∴DB=AE,
又∵DB∥AC,
∴四边形DBEA是平行四边形(一组对边平行且相等的四边形是平行四边形),
∵AB=BC,E为AC中点,
∴∠AEB=90°,
∴平行四边形DBEA是矩形,
即△ABC满足AB=BC时,四边形DBEA是矩形.
∴EC=
| 1 |
| 2 |
∵DB=
| 1 |
| 2 |
∴DB=EC,
又∵DB∥AC,
∴四边形BCED是平行四边形(一组对边平行且相等的四边形是平行四边形),
∴BC=DE;
(2)解:△ABC满足AB=BC时,四边形DBEA是矩形.

理由如下:∵E是AC的中点,
∴AE=
| 1 |
| 2 |
∵DB=
| 1 |
| 2 |
∴DB=AE,
又∵DB∥AC,
∴四边形DBEA是平行四边形(一组对边平行且相等的四边形是平行四边形),
∵AB=BC,E为AC中点,
∴∠AEB=90°,
∴平行四边形DBEA是矩形,
即△ABC满足AB=BC时,四边形DBEA是矩形.
点评:本题考查了矩形的判定,平行四边形的判定与性质,等腰三角形三线合一的性质,题目难度不大,熟练掌握平行四边形的判定与性质以及平行四边形与矩形的联系是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 如图,DB∥AC,且DB=
如图,DB∥AC,且DB= 如图,DB∥AC,且DB=
如图,DB∥AC,且DB=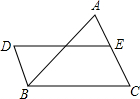 如图,DB∥AC,且DB=
如图,DB∥AC,且DB=