题目内容
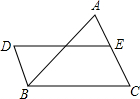 如图,DB∥AC,且DB=
如图,DB∥AC,且DB=| 1 | 2 |
(1)求证:BC=DE;
(2)连接AD、BE,若要使四边形ADBE是菱形,则给△ABC添加什么条件,并说明理由.
分析:(1)可先判定四边形DBCE是平行四边形,根据平行四边形的性质可得到结论.
(2)添加∠ABC=90°,可判断出一组邻边相等,一组邻边相等的平行四边形是菱形.
(2)添加∠ABC=90°,可判断出一组邻边相等,一组邻边相等的平行四边形是菱形.
解答: (1)证明:∵E是AC的中点
(1)证明:∵E是AC的中点
∴EC=
AC
∵DB=
AC
∴DB=EC …(1分)
又∵DB∥AC
∴四边形DBCE是平行四边形…(3分)
∴BC=DE …(4分)
(2)添加∠ABC=90° …(5分)
理由:∵DB=AE,DE∥AC
∴四边形ADBE是平行四边形…(6分)
∵∠ABC=90°
∴在Rt△ABC中,E是斜边AC的中点
∴AE=EB
∴四边形DBEA是菱形 …(8分)
 (1)证明:∵E是AC的中点
(1)证明:∵E是AC的中点∴EC=
| 1 |
| 2 |
∵DB=
| 1 |
| 2 |
∴DB=EC …(1分)
又∵DB∥AC
∴四边形DBCE是平行四边形…(3分)
∴BC=DE …(4分)
(2)添加∠ABC=90° …(5分)
理由:∵DB=AE,DE∥AC
∴四边形ADBE是平行四边形…(6分)
∵∠ABC=90°
∴在Rt△ABC中,E是斜边AC的中点
∴AE=EB
∴四边形DBEA是菱形 …(8分)
点评:本题考查了平行四边形的判定和性质,菱形的判定,以及直角三角形中斜边中线的性质等知识点.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
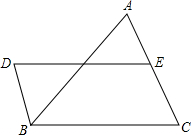 如图,DB∥AC,且DB=
如图,DB∥AC,且DB= 如图,DB∥AC,且DB=
如图,DB∥AC,且DB= 如图,DB∥AC,且DB=
如图,DB∥AC,且DB=