题目内容
19.分解因式:x2-5x+2=(x-$\frac{5}{2}$+$\frac{\sqrt{17}}{2}$)(x-$\frac{5}{2}$-$\frac{\sqrt{17}}{2}$).分析 首先可将原式变形为(x-$\frac{5}{2}$)2-$\frac{17}{4}$,再利用平方差公式分解即可求得答案.
解答 解:x2-5x+2
=x2-5x+$\frac{25}{4}$-$\frac{25}{4}$+2
=(x-$\frac{5}{2}$)2-$\frac{17}{4}$
=(x-$\frac{5}{2}$+$\frac{\sqrt{17}}{2}$)(x-$\frac{5}{2}$-$\frac{\sqrt{17}}{2}$).
故答案为:(x-$\frac{5}{2}$+$\frac{\sqrt{17}}{2}$)(x-$\frac{5}{2}$-$\frac{\sqrt{17}}{2}$).
点评 本题考查了实数范围内的因式分解.注意此题将原式变形为(x-$\frac{5}{2}$)2-$\frac{17}{4}$是关键.

练习册系列答案
相关题目
9.“a<b”的反面是( )
| A. | a≠b | B. | a>b | C. | a=b | D. | a≥b |
7.以下各数中,填入□中能使(-$\frac{1}{2}$)×□=-2成立的是( )
| A. | -1 | B. | 2 | C. | 4 | D. | -4 |
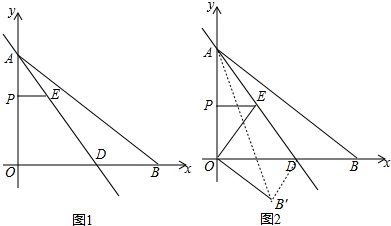
 ”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为4a-8b.
”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为4a-8b.