题目内容
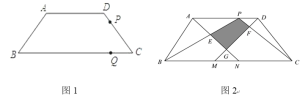
【题目】如图1,等边三角形![]() 中,D为
中,D为![]() 边上一点,满足
边上一点,满足![]() ,连接
,连接![]() ,以点A为中心,将射线
,以点A为中心,将射线![]() 顺时针旋转60°,与
顺时针旋转60°,与![]() 的外角平分线
的外角平分线![]() 交于点E.
交于点E.
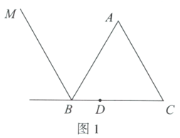
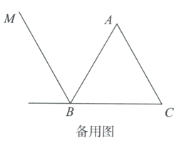
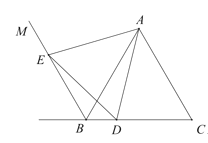
(1)依题意补全图1;
(2)求证:![]() ;
;
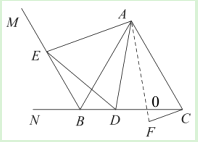
(3)若点B关于直线![]() 的对称点为F,连接
的对称点为F,连接![]() .
.
①求证:![]() ;
;
②若![]() 成立,直接写出
成立,直接写出![]() 的度数为_________°.
的度数为_________°.
【答案】(1)图见解析;(2)证明见解析;(3)①证明见解析; ②20°.
【解析】
(1)根据题意,射线![]() 顺时针旋转60°,用尺规作图法,做出∠DAE = ∠C = 60°,再连接DE,即完成作图;
顺时针旋转60°,用尺规作图法,做出∠DAE = ∠C = 60°,再连接DE,即完成作图;
(2)在等边三角形ABC中,由![]() 可得出
可得出![]() ;由射线
;由射线![]() 绕点A顺时针旋转60°得到射线
绕点A顺时针旋转60°得到射线![]() ,可得∠DAE =
,可得∠DAE =![]() ,进而得出
,进而得出![]() ;由
;由![]() 平分∠ABC的外角
平分∠ABC的外角![]() 可得
可得![]() ,进而推出
,进而推出![]() ,由此可证
,由此可证![]() (ASA),再根据三角形全等的性质易证
(ASA),再根据三角形全等的性质易证![]() ;
;
(3)①连接![]() ,设
,设![]() ,根据点B与点F关于直线
,根据点B与点F关于直线![]() 对称的性质可得
对称的性质可得![]() ,
,![]() ;由
;由![]() 易得
易得![]() ;在等边三角形
;在等边三角形![]() 中, 由
中, 由![]() ,
,![]() ,易证
,易证![]() ,
,![]() ,又因为
,又因为![]() ,再根据三角形AFC的内角和定理,可推出
,再根据三角形AFC的内角和定理,可推出![]() ,和前面的证明联立可得
,和前面的证明联立可得![]() ,所以同旁内角互补,
,所以同旁内角互补,![]() .
.
②通过图中各个三角形的内角和之间的关系,设∠BAD=α,通过证明∠CFA=∠COF推论出![]() ,即可计算出∠BAD=20°.
,即可计算出∠BAD=20°.
(1)依题意补全图形
(2)证明:
∵![]() 是等边三角形,
是等边三角形,
∴![]() .
.
∴![]() .
.
∵射线![]() 绕点A顺时针旋转60°得到射线
绕点A顺时针旋转60°得到射线![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() 平分
平分![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.

(3)①证明:连接![]() ,设
,设![]() ,
,
∵点B与点F关于直线![]() 对称,
对称,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∵等边三角形![]() 中,
中,![]() ,
,
∴![]()
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
且![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
② 由① 知 ![]() ,
,![]()
∴∠EAF=∠F=![]()
∴∠DAF = α,
∵![]() ,由②知BE=CD
,由②知BE=CD
∴BD=CF
∴∠CFA=∠COF
∴![]()
∴3α=60°
∴α=20°

练习册系列答案
相关题目