题目内容
11.已知Rt△ABC中,斜边AB=2,tanB=$\frac{4}{3}$,则AC=$\frac{8}{5}$.分析 根据tanB=$\frac{4}{3}$,设出AC=4x,则BC=3x,根据勾股定理求出x的值,从而得出AC.
解答  解:如图,∵tanB=$\frac{AC}{BC}$=$\frac{4}{3}$,
解:如图,∵tanB=$\frac{AC}{BC}$=$\frac{4}{3}$,
∴设AC=4x,则BC=3x,
∵△ABC是直角三角形,
∴AC2+BC2=AB2,
∵AB=2,
∴16x2+9x2=4,
解得:x1=$\frac{2}{5}$,x2=-$\frac{2}{5}$(不合题意,舍去),
∴AC=4x=4×$\frac{2}{5}$=$\frac{8}{5}$.
故答案为:$\frac{8}{5}$.
点评 此题考查了解直角三角形,用到的知识点是特殊角的三角函数值和勾股定理,关键是根据题意设出AC=4x,得出BC=3x.

练习册系列答案
相关题目
1. 在平面直角坐标系xOy中,已知点A(2,3),在x轴上找一点P,使得△AOP是等腰三角形,则这样的点P共有( )个.
在平面直角坐标系xOy中,已知点A(2,3),在x轴上找一点P,使得△AOP是等腰三角形,则这样的点P共有( )个.
 在平面直角坐标系xOy中,已知点A(2,3),在x轴上找一点P,使得△AOP是等腰三角形,则这样的点P共有( )个.
在平面直角坐标系xOy中,已知点A(2,3),在x轴上找一点P,使得△AOP是等腰三角形,则这样的点P共有( )个.| A. | 4 | B. | 5个 | C. | 7个 | D. | 8个 |
 如图,已知在△ABC中,AB=AC,AD⊥BC于点D,AD=4cm,△ABC的周长为16cm,求AB的长.
如图,已知在△ABC中,AB=AC,AD⊥BC于点D,AD=4cm,△ABC的周长为16cm,求AB的长.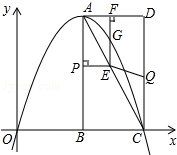 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.