题目内容
已知点P(1,-2a)在二次函数y=ax2+6的图象上,并且点P关于x轴的对称点在反比例函数 的图象上。
的图象上。
(1)求此二次函数和反比例函数的解析式;
(2)点(-1,4)是否同时在(1)中的两个函数图象上?
【解析】
(1)∵点P(1,-2a)在二次函数y=ax2+6的图象上,
∴-2a=a+6,
解得,a=-2.
∴点P为(1,4),所求二次函数解析式为y=-2x2+6.
点P关于x轴对称点的坐标为(1,-4),
把(1,-4)代入 ,
,
∴k=-4,故所求反比例函数解析式为y=? .
.
(2)点(-1,4)既在y=-2x2+6图象上,也在y=? 图象上.
图象上.
【解析】
试题分析:(1)将点P(1,-2a)代入二次函数y=ax2+6,解方程即可求出a的值,从而求出点P关于x轴的对称点坐标,代入解析式即可求出k的值,从而得到函数解析式;(2)将点(-1,4)分别代入两个函数的解析式,若同时成立,则同时在(1)中的两个函数图象上.
考点:二次函数图象上点的坐标特征;反比例函数图象上点的坐标特征.

练习册系列答案
相关题目
对于抛物线  .
.
(1)它与x轴交点的坐标为 ,与y轴交点的坐标为 ,顶点坐标为 ;
(2)在坐标系中利用描点法画出此抛物线;

x | … | … | |||||
y | … | … |
(3)利用以上信息解答下列问题:若关于x的一元二次方程 (t为实数)在
(t为实数)在 <x<
<x< 的范围内有解,则t的取值范围是 .
的范围内有解,则t的取值范围是 .
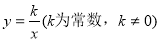 的图像可能是( )
的图像可能是( )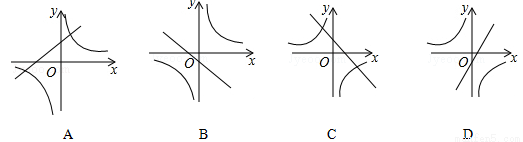

 ;
;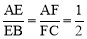 ,则△EFD与△ABC的面积比为( )
,则△EFD与△ABC的面积比为( )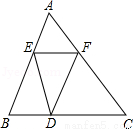
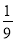 B.
B.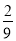 C.
C.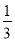 D.
D.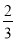
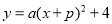 的图象是由函数
的图象是由函数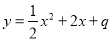 的图象向左平移一个单位得到.反比例函数
的图象向左平移一个单位得到.反比例函数 与二次函数
与二次函数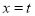 的一侧都是y随着x的增大而减小,求t的最大值;
的一侧都是y随着x的增大而减小,求t的最大值;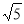 ,求出点D,C的坐标.
,求出点D,C的坐标. B.
B. C.
C. D.
D.