题目内容
4. 如图,△ABC中,∠C=90°,AC=BC=2,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2.照此规律作下去,则S2016=$\frac{1}{{4}^{2015}}$.
如图,△ABC中,∠C=90°,AC=BC=2,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2.照此规律作下去,则S2016=$\frac{1}{{4}^{2015}}$.
分析 根据三角形中位线定理可求出S1的值,进而可得出S2的值,找出规律即可得出S2016的值.
解答 解:∵∠C=90°,AC=BC=2,
∴S△ABC=$\frac{1}{2}$AC•BC=2,解:∵E是BC的中点,ED∥AB,
∴DE是△ABC的中位线,
∴DE=$\frac{1}{2}$AB,
∴S△DCE=$\frac{1}{4}$S△ABC.
同理,S△BEF=$\frac{1}{4}$S△ABC.
∴S1=S△ABC-S△DCE-S△BEF=$\frac{1}{2}$×S△ABC,
同理求得S2=$\frac{1}{{2}^{3}}$×S△ABC,
…
Sn=$\frac{1}{{2}^{2n-1}}$•S△ABC,
S2016×S△ABC=$\frac{1}{{2}^{4032}}$×2=$\frac{1}{{4}^{2015}}$,
故答案为:$\frac{1}{{4}^{2015}}$.
点评 本题考查了三角形中位线定理、等边三角形的性质.三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
相关题目
12.若多项式x2+ax+9恰好是另一个多项式的平方,则a值( )
| A. | ±6 | B. | -6 | C. | 3 | D. | ±3 |
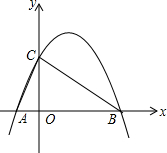 如图,已知抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B两点(A左、右B),与y轴交于点C.
如图,已知抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B两点(A左、右B),与y轴交于点C. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,-1),B(-1,1),C(0,-2).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,-1),B(-1,1),C(0,-2).