题目内容
 已知?ABCD的两邻边上的高AE=2,AF=3,∠B=45°,则?ABCD的面积为
已知?ABCD的两邻边上的高AE=2,AF=3,∠B=45°,则?ABCD的面积为考点:平行四边形的性质
专题:
分析:由?ABCD的两邻边上的高AE=2,AF=3,∠B=45°,可求得边AB的长,继而求得答案.
解答:解:∵高AE=2,∠B=45°,
∴BE=AE=2,
∴AB=
=2
,
∵四边形ABCD是平行四边形,
∴CD=AB=2
,
∵高AF=3,
∴?ABCD的面积为:CD•AF=2
×3=6
.
故答案为:6
.
∴BE=AE=2,
∴AB=
| AE2+BE2 |
| 2 |
∵四边形ABCD是平行四边形,
∴CD=AB=2
| 2 |
∵高AF=3,
∴?ABCD的面积为:CD•AF=2
| 2 |
| 2 |
故答案为:6
| 2 |
点评:此题考查了平行四边形的性质以及勾股定理.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
下列四个实数中,绝对值最小的数是( )
| A、-5 | ||
| B、-π | ||
C、
| ||
| D、4 |
下列命题是真命题的是( )
| A、对顶角相等 |
| B、底边相等的两个等腰三角形全等 |
| C、同位角相等 |
| D、两个锐角的和一定是钝角 |
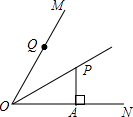 如图,如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=10,则PQ的最小值为( )
如图,如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=10,则PQ的最小值为( )| A、5 | B、10 | C、15 | D、20 |
 如图是“北大西洋公约组织”标志的主体部分(平面图),它是由8个完全相同的三角形拼接而成的.测得∠ABO=20°,则∠ECO的度数是( )
如图是“北大西洋公约组织”标志的主体部分(平面图),它是由8个完全相同的三角形拼接而成的.测得∠ABO=20°,则∠ECO的度数是( )| A、115° | B、116° |
| C、117° | D、137.5° |
在-1
,12,-20,0,-(-5)中,负数的个数有( )
| 1 |
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |